基本路径测试法
基本路径测试法是在是在程序控制流图的基础上,通过分析控制构造的环路复杂性,导出基本可执行路径 出基本可执行路径集合,从而设计测试用例的方法。设计出的测试用例要保证在测试中程序的每一条可执行语句至少执行一次。
程序的控制流图
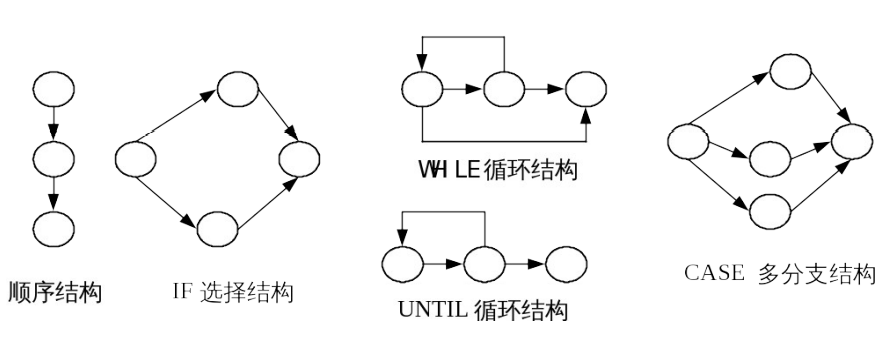
控制流图是描述程序控制流的一种图示方式。其中基本的控制结构对应的图形符号如图所示。在图所示的图形符号中,圆圈称为控制流图的一个结点,它表示一个或多个无分支的语句或源程序语句。
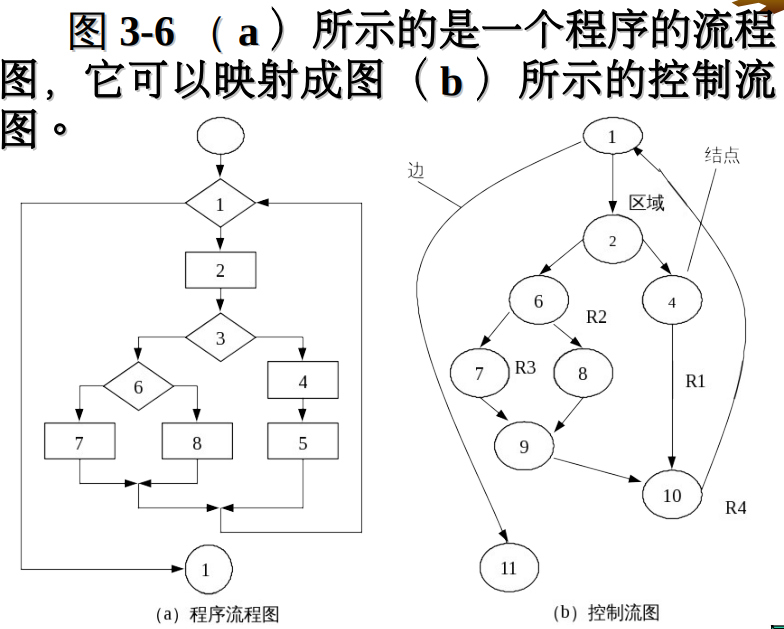
如下图所示,程序的流程图可以映射到控制流图
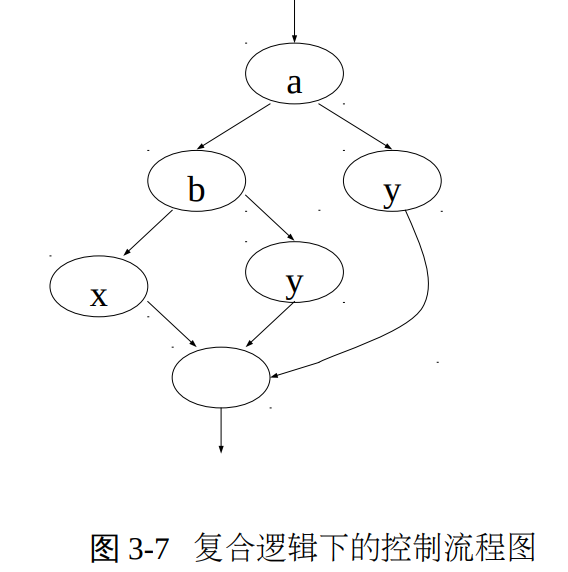
在具有复合条件的情况时,可以转化拆分成成单条件的流程图,如下图先判断单条件a,则根据短路直接可执行到y,否则继续判断b
环路复杂度
进行程序的基本路径测试 进行程序的基本路径测试时,程序的环路复杂性给出了程序基本路径集合中的独立路径条数,这是确保程序中每个可执行语句至少执行一次所必须的测试用例数的测试用例数目的最小值。
所谓独立路径,是指包括若干未曾处理的语句或条件的一条路径。
基本路径集不是惟一的,对于给定的控制流图,可以得到不同的基本路径集。
通常环路复杂性可用以下3种方法求得。
-
将环路复杂J性定义为控制流图中的区域数
-
设 E 为控制流图的边数, N 为图的结点数,则定义环路的复杂性为 V(G)=E−N+2
-
若设 P为控制流图中的判定结点数,则有 V(G)=P+1
基本路径测试法的步骤
-
画出程序的控制流图
-
计算程序的环路复杂度
-
确定独立路径的集合
-
准备测试用例
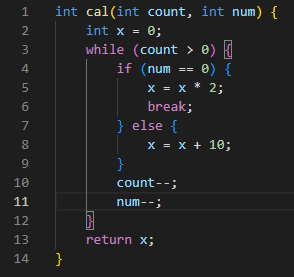
例题1
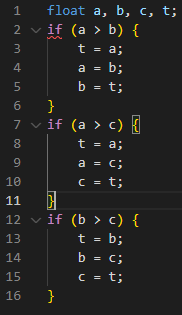
代码
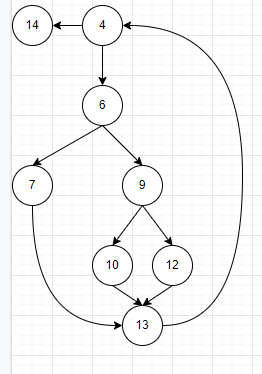
控制流图
环路复杂度
-
直接数封闭区域,
-
6-7-13-10-9-6
-
9-10-13-12-9
-
4-6-9-12-13-4
-
外围区域
-
-
判定节点为4, 6, 9,则判定节点数+1为4
-
顶点数有7个,边有9条,则有9-7+2=4
独立路径
路径1: 4-14
路径2: 4-6-7-13-4-14
路径3: 4-6-9-10-13-4-14
路径4: 4-6-9-12-13-4-14
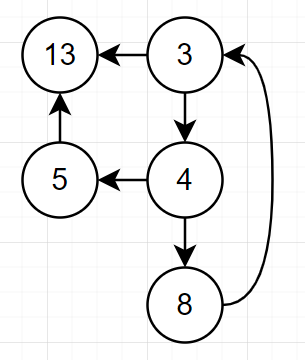
例题2
代码
控制流图
环路复杂度
-
直接数封闭区域,
-
3-4-5-13-3
-
3-4-8-3
-
外围区域
-
-
判定节点为3, 4,则判定节点数+1为3
-
顶点数有5个,边有6条,则有6-5+2=3
独立路径
路径1: 3-13
路径2: 3-4-5-13
路径3: 3-4-8-13
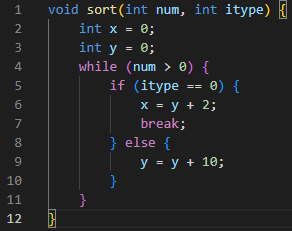
例题3
代码
控制流图
环路复杂度
-
直接数封闭区域,
-
4-5-9-4
-
4-5-7-12-4
-
外围区域
-
-
判定节点为4, 5,则判定节点数+1为3
-
顶点数有5个,边有6条,则有6-5+2=3
独立路径
路径1: 4-12
路径2: 4-5-9-12
路径3: 4-5-7-12
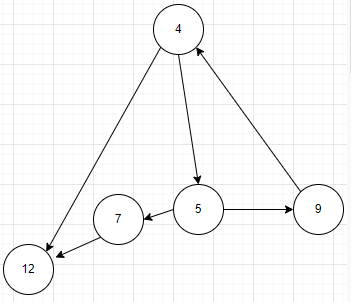
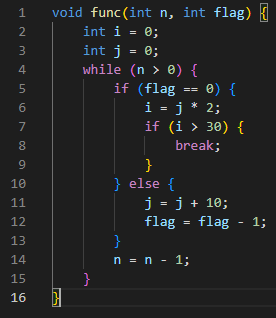
例题4
代码
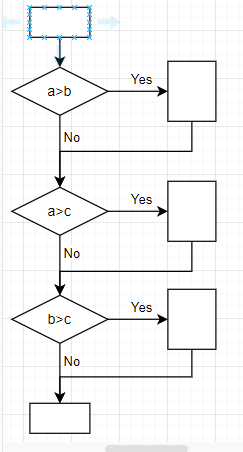
流程图
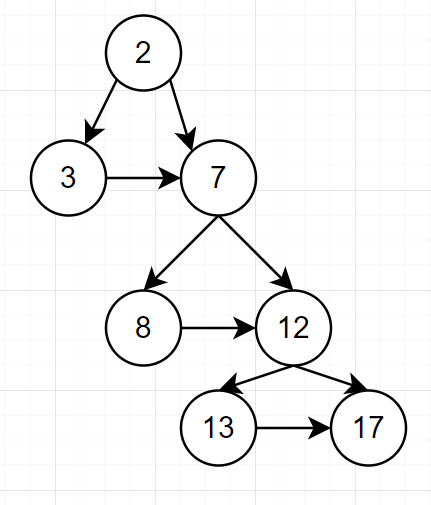
控制流图
环路复杂度
-
直接数封闭区域,
-
2-3-7-2
-
7-8-12-7
-
12-13-17-12
-
外围区域
-
-
判定节点为2, 7, 12,则判定节点数+1为4
-
顶点数有7个,边有9条,则有9-7+2=4
基本路径
路径1: 2-7-12-17
路径2: 2-3-7-12-17
路径3: 2-7-8-12-17
路径4: 2-7-12-13-17
例题5
代码
控制流图
环路复杂度
-
直接数封闭区域,
-
4-5-7-16-4
-
4-5-13-14-4
-
5-7-14-13-5
-
外围区域
-
-
判定节点为4, 5, 7,则判定节点数+1为4
-
顶点数有6个,边有8条,则有8-6+2=4
独立路径
路径1: 4-16
路径2: 4-5-7-16
路径3: 4-5-7-14-4-16
路径4: 4-5-13-14-4-16
设计测试用例
路径1: n=0
路径2: n=100, flag = 2
路径3: n=2, flag = 1
路径4: n=1, flag=1
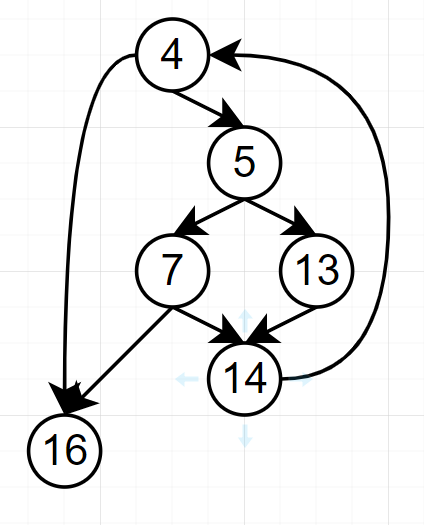
例题6
代码
1 | 1 int Test(int num, int x) |
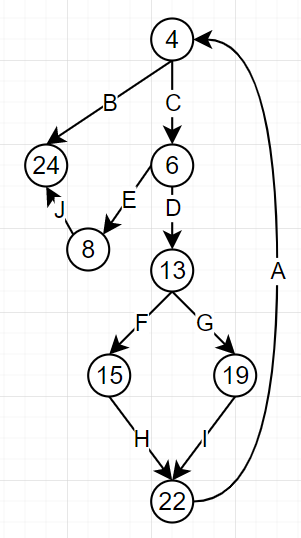
控制流图
环路复杂度
-
直接数封闭区域,
-
4-6-13-15-22-4
-
4-6-8-24-4
-
13-15-22-19-13
-
外围区域
-
-
判定节点为4, 6, 13,则判定节点数+1为4
-
顶点数有8个,边有10条,则有10-8+2=4
独立路径
路径1: B (4-24)
路径2: C-E-J (4-6-8-24)
路径3: C-D-G-I-A-B (4-6-13-15-22-4-24)
路径4: C-D-F-H-A-B (4-6-13-19-22-4-24)
设计测试用例
路径1
-
输入:num <= 0 的某个值
-
输出:temp = 0
路径2
-
输入:num>0的任意值, x>0的任意值
-
输出:temp=num+100
路径3
-
输入:x=0, num=1
-
输出:temp=10
路径4
-
输入:x=-1, num=1
-
输出:temp=20
等价类划分法
等价类划分是一种典型的、常用的黑盒测试方法。
所谓等价类是指某个输入域的子集,使用这一方法 ,使用这一方法时,是把所有可能的输入数据,即程序的输入域划分成若干
部分(子集),然后从每一个子集中选取少数具有代表性的数据作为测试用例。
等价类划分的情况
等价类的划分有以下两种不同的情况
-
有效等价类:是指对于程序规格说明来说,是合理的、有意义的输入数据构成的集合。利用它,可以检验程序是否实现了规格说明预先规定的功能和性能。
-
无效等价类 :是指对于程序规格说明来说,是不合理的、无意义的输入数据构成的集合。利用它,可以检查程序中功能和性能的实现是否有不符合规格说明要求的地方
划分等价类的方法
-
按区间划分
-
按数值划分
-
按数值集合划分
-
按限制条件划分
-
按限制规则划分
-
按处理方式划分
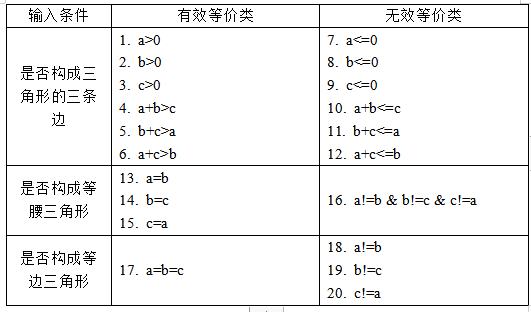
在确立了等价类之后,建立等价类表,列出所有划分出的等价类,如表 3-1 所示
再从划分出的等价类中按以下原则选择测试用例。 选择测试用例。
-
为每一个等价类规定一个唯一的编号
-
设计一个新的测试用例,使其尽可能多地覆盖尚未覆盖的有效等价类;重复这一步骤,直到所有的有效等价类都被覆盖为止。
-
设计一个新的测试用例,使其 设计一个新的测试用例,使其仅覆盖一个无效等价类,重复这一步骤,直到所有的无效等价类都被覆盖为止。
三角形问题
三角形问题是软件测试文献中使用最广泛的一个例子。
三角形问题之所以复杂,是因为输入与输出之间的关系比较复杂。
问题概述
输入三个整数a,b,c分别作为三角形的三条边,程序判断由这三条边构成的三角形类型是:等边三角形,等腰三角形,一般三角形或非三角形。
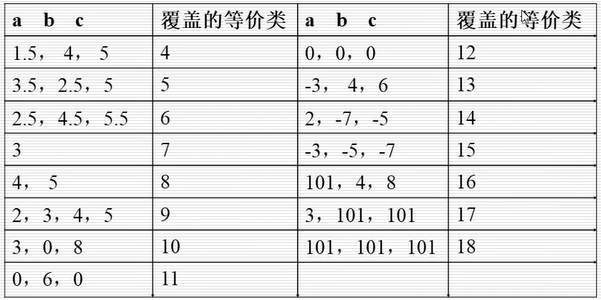
传统等价类划分测试用例设计
设输入条件分别要求为(这些输入条件自身都作为了有效等价类):
-
整数(设为1号有效等价类)
-
有一条边为非整数,设为4号无效等价类
- 1.5, 4, 5
-
有两条边为非整数,设为5号无效等价类
- 3.5, 2.5, 5
-
有三条边为非整数,设为6号无效等价类
- 2.5, 4.5, 5.5
-
-
三个数(设为2号有效等价类)
-
只有一条边,设为7号无效等价类
- 3
-
只有两条边,设为8号无效等价类
- 4, 5
-
多于三条边,设为9号无效等价类
- 2, 3, 4, 5
-
-
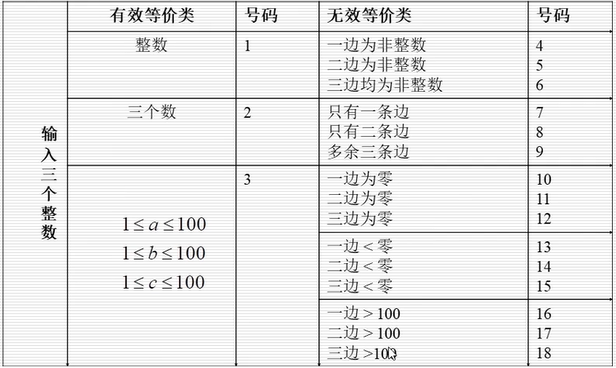
三个数取值分别为1到100(设为3号有效等价类)
-
一边=0,设为10号
- 3, 0, 8
-
二边=0,设为11号
- 0, 6, 0
-
三边=0,设为12号
- 0, 0, 0
-
一边<0,设为13号
- -3, 4, 6
-
两边<0,设为14号
- 2, -7, -5
-
三边<0,设为15号
- -3, -5, -7
-
一边>100,设为16号
- 101, 4, 8
-
二边>100,设为17号
- 3, 101, 101
-
三边>100,设为18号
- 101, 101, 101
-
等价类划分表
为无效等价类设计测试用例表
标准和健壮等价类划分测试用例设计
三角形问题有四种可能输出:
-
非三角形
-
一般三角形
-
等腰三角形
-
等边三角形
利用这些信息来确定输出(值域)等价类。
R1={<a, b, c>: 边为a, b, c的等边三角形}
R2={<a, b, c>: 边为a, b, c的等腰三角形}
R3={<a, b, c>: 边为a, b, c的一般三角形}
R4={<a, b, c>: 边a, b, c不能形成三角形}
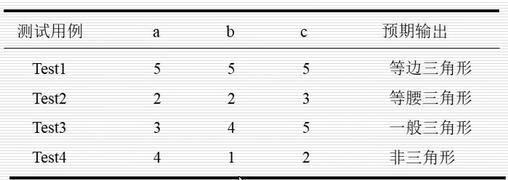
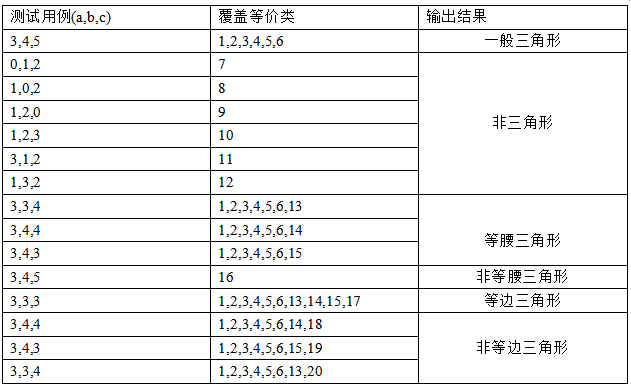
可以设计四个标准等价类如下,
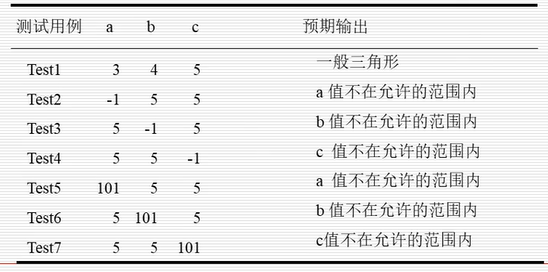
考虑a, b, c的无效值产生了下面7个健壮等价类测试用例,如下表所示:
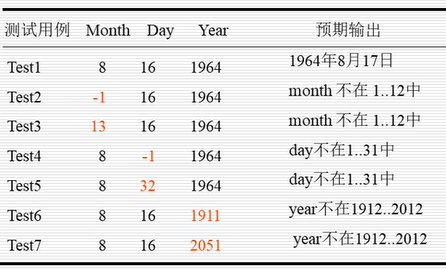
NextDate问题
NextDate是一个含三个变量month, day, year的函数。有效值区间定义如下:
-
M1={month: 1<=month<=12}
-
D1={day: 1<=day<=31}
-
Y1={year: 1912<=year<=2050}
无效等价类为:
-
M2={month: month < 1}
-
M3={month: month > 12}
-
D2={day: day < 1}
-
D3={day: day>31}
-
Y2={year: year < 1912}
-
Y3={year: year > 2050}
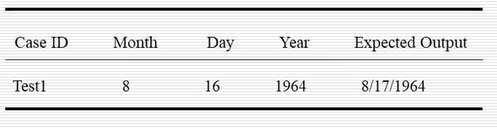
只有一个标准等价类的测试用例
健壮等价类测试用例
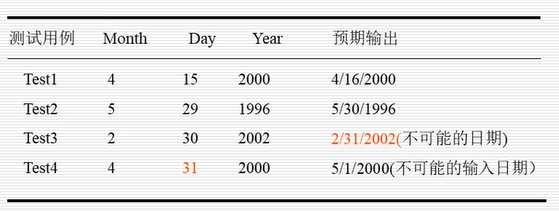
如果更仔细地选择等价关系,可以得到更有用的等价类:
标准等价类测试用例
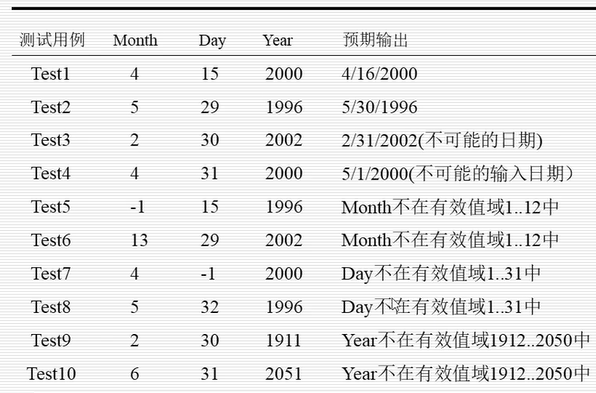
健壮等价类测试用例
边界值分析法
边界值分析法就是对输入或输出的边界值进行测试的一种黑盒测试方法。
在测试过程中,边界值分析法是通过选择等价类边界的测试用例进行测试,边界值分析法与等价类划分法的区别是边界值分析不是从某等价类中随便挑一个作为代表,而是使这个等价类的每个边界都要作为测试条件。
另外,边界值分析不仅考虑输入条件边界,还要考虑输出条件边界,还要考虑输出域边界产生的测试情况。
使用边界值分析方法设计测试用例,首先应确定边界情况。
通常输入等价类与输出等价类的边界,就是应着重测试的边界情况。应当选取正好等于,刚刚大于,或刚刚小于边界的值作为测试数据,而不是选取等价类中的典型值或任意值作为测试数据
选择测试用例的原则
-
如果输入条件规定了值的范围,则应该取刚达到这个范围的边界值,以及刚刚超过这个范围边界的值作为测试输入数据。
-
如果输入条件规定了值的个数,则用最大个数、最小个数、比最大个数多 1 个、比最小个数少 1 个的数作为测试数据。
-
根据规格说明的每一个输出 据规格说明的每一个输出条件,使用前面两条规则 。
-
如果程序的规格说明 如果程序的规格说明给出的输入域或输出域是有序集合(如有序表、 顺序文件等),则应选取集合的第一个和最后一个元素作为测试用例。
-
如果程序用了一个内部结构,应该选取这个内部数据结构的边界值作为测试用例。
-
分析规格说明, 分析规格说明,找出其他可能的边界条件。
因果图法
因果图法是一种利用图解法分析输入的各种组合情况,从而设计测试用例的方法,它适合于检查程序输入条件的各种组合情况。
利用因果图生成测试用例的基本步骤如下:
-
分析软件规格说明的描述中哪些是原因,哪些是结果。原因是输入条件或输入条件的等价类,结果是输出条件。
-
分析软件规格说明描述中的语义,找出原因与结果之间、原因与原因之间对应的关系,根据这些关系,画出因果图。
-
标明约束条件。由于语法或环境的限制,有些原因和结果的组合情况是不可能出现的。为表明这些特定的情况,在因果图上使用若干标准的符号标明约束条件
-
把因果图转换成判定表
-
为判定表中的每一列设计测试用例
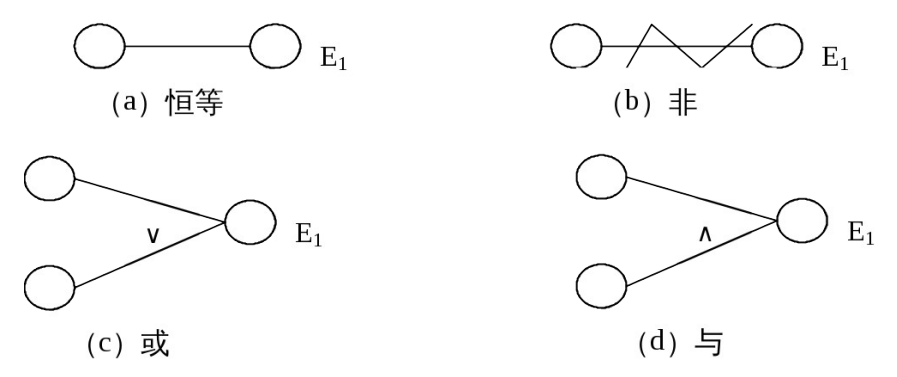
通常在因果图中,用 Ci表示原因, Ei表示结果,其基本符号如图 3-15 所示。
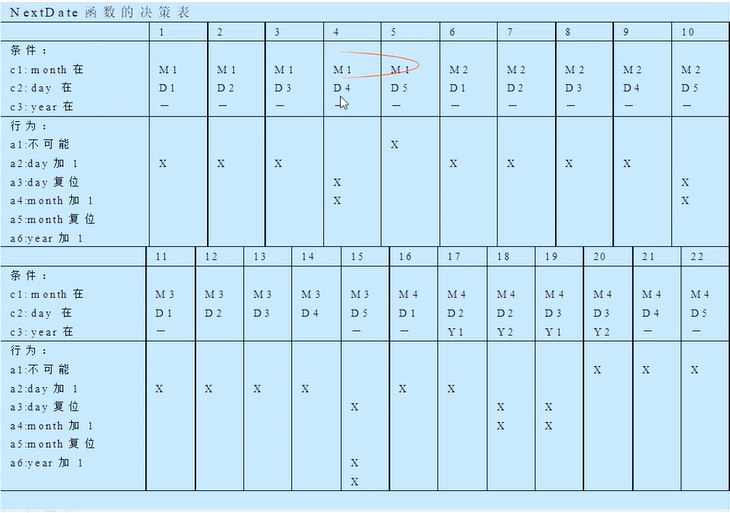
决策表法
NextDate问题
NextDate函数能够使用的操作只有5种
Day变量+1
Month变量+1
Day变量复位
Month变量复位
Year变量+1
将注意力集中到NextDate函数的日月问题上,并仔细研究动作桩,可以在以下等价类集合上建立决策表:
集成测试的实施方案
集成测试的实施方案有很多种,如:
非增式集成测试和增量式集成测试、 量式集成测试、三明治集成测试、核心集成测试、分层集成测试、基于使用的集成测试等。其中,常用的是非增式集成测试和增量式集成测试两种模式。
非增式测试方法
概括来说,非增式测试方法是采用一步 式测试方法是采用一步到位的方法来进行测试,对所有模块进行个别的单元测试后,按程序结构图将各模块程序结构图将各模块连接起来,把连接后的程序当做一个整体进行测试。图 4-4 给出的是采用这种非增式的集成测试方法的一个经典例子。
增式测试方法
自顶向下增式测试
自顶向下增式测试表示逐步集成和逐步测试是按结构图自上而下进行的。即模块集成的顺序是首先集成主控模块(主程序),然后按照软件控制层次结构向下进行集成。
集成测试的整个过程由下列 3 个步骤完成:
-
主控模块作为测试驱动器,把对主控模块进行单元测试时引入的被调用模拟子模块用实际模块替代。
-
依照所选用的模块集成策略(深度优先和广度优先),下层的被调用模拟子模块一次一个地被替换为真正的模块。
-
在每个模块被集成时, 在每个模块被集成时,都必须立即进行测试一遍,回到第 2 步重复进行,直到整个系统结构被集成完成。
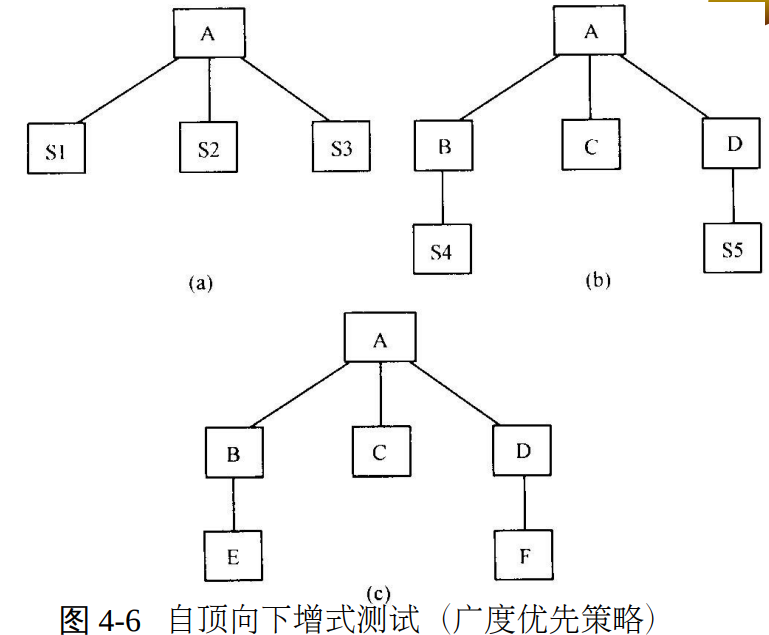
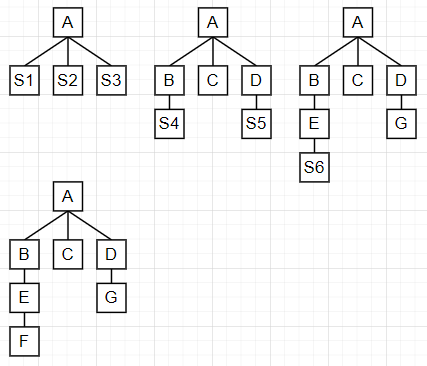
图 4-6 给出了一个按广度优先策略进行集成测试的典型例子:
开发模块A时,使用用于支撑测试的桩模块S1,S2,S3,然后将S1,S2,S3分别替换为真正的模块B,C,D,其中模块S4,S5依然使用桩模块支撑,最后再替换桩模块S4,S5为模块E,F,最终集成测试完毕。
自底向上增式测试
自底向上增式测试是从最底层的模块开始,按结构图自下而上逐步进行集成和测试。
图 4-7 表示了采用自底向上增式测试实现同一实例的过程。
其他集成测试实施方案
-
三明治集成测试
-
核心系统先行集成测试
-
高频集成测试
各种例题
功能描述:如果x<=3000,y的值为0;如果3000<x<=5000,则y的值为x超过3000部分的3%;如果5000<x<8000,则y 的值为:x超过5000部分的5%加上超过3000部分的3%。
请用等价类划分和边界值分析相结合来设计测试用例。
由题意得
- x<=3000
- y=0
- 3000<x<=5000
- y=0.03*x-90
- 5000<x<8000
- y=0.08*x-340
- x>=8000
- 未定义
有效等价类
- x<=3000
- 3000<x<=5000
- 5000<x<8000
无效等价类
- x>=8000
测试用例
应该取边界值2999, 3000, 3001, 4999, 5000, 5001, 7999, 8000, 8001
2999, 3000=>0: 覆盖1
3001,4999,5000=>0.03, 59.97, 60: 覆盖2
5001, 7999=>60.08, 299.92: 覆盖3
8000, 8001: 覆盖4
功能描述:密码输入框的字符长度要求为最短4个字符,最长20个字符。 请用等价类划分和边界值分析相结合来设计测试用例。(要考虑字符的类型)
长度的边界值3,4,5, 19,20,21
类型有三种纯数字,纯字母,数字+字母
有效等价类
-
4-20字符
-
纯数字
-
纯字母
-
数字+字母
无效等价类
-
少于4字符
-
多于20字符
-
含有特殊符号
设计测试用例
设计一个新的测试用例,使其尽可能多地覆盖尚未覆盖的有效等价类;重复这一步骤,直到所有的有效等价类都被覆盖为止。
设计一个新的测试用例,使其设计一个新的测试用例,使其仅覆盖一个无效等价类,重复这一步骤,直到所有的无效等价类都被覆盖为止。
123: 覆盖了2, 5
abcd: 覆盖了1,3
abcdefghij1234567890: 覆盖了1, 4
abcdefghij12345678901: 覆盖了4, 6
abcdefghij123456789-: 覆盖了1, 7
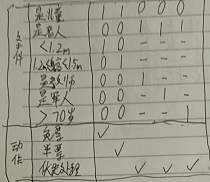
“……对1.2米以下儿童免票,对1.2-1.5米的儿童半票,对教师、军人或70岁以上的老人,应给予优先的业务处理……”
这里假设“优先的业务处理”已在别处有更严格的定义,请建立判定表。
-
是儿童
-
<1.2米 => 免票
-
1.2-1.5米 => 半票
-
-
是老人
-
是教师 => 优先业务处理
-
是军人 => 优先业务处理
-
70岁以上 => 优先业务处理
-
请用等价类划分法设计测试用例。
1 | void triangle(float a, float b, float c) { |
参考后面也有同样的题
请用等价类划分法设计下列代码的单元测试用例。
1 | float jisuan(float a) { |
有效等价类
-
800 <a<=2000
-
2000<a<=5000
-
a>5000
无效等价类
- a<=800
边界值
799,800,801,1999,2000,2001,4999,5000,5001
测试用例
799, 800: 覆盖4
801, 1999, 2000: 覆盖1
2001, 4999, 5000: 覆盖2
5001: 覆盖3
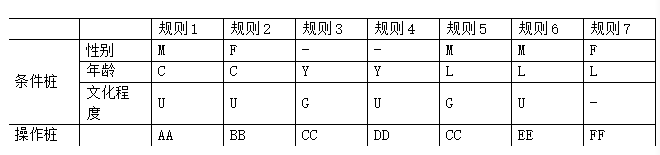
某单位对其在大学以上学历的职工安排工作(工作岗位用AA-FF表示),方针如下:
-
如果年龄不满18岁,文化程度为大学,若是男性,则任AA。若是女性,则任BB;
-
如果年满18但不足50岁,文化程度是研究生,不分男女性,均任CC。文化程度是大学,则不分男女性均任DD;
-
如果年满50岁以上,文化程度是研究生,若是男性,则任CC,文化程度是大学,若是男性,则任EE。若是女性,则任FF。
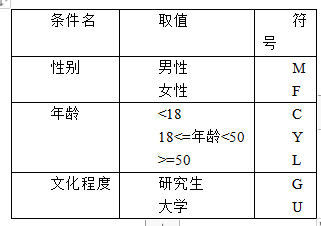
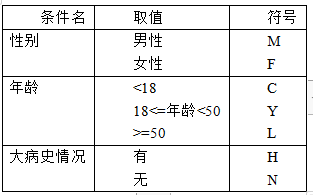
请对以上说明绘制判定表。为了便于绘制,条件符号使用以下内容:
-
不满18岁 C
-
大学 U
-
男性 M => AA
-
女性 F => BB
-
-
研究生 G
- 未知 => X
-
-
年满18岁未满50岁 Y
-
研究生 G
-
男性 M => CC
-
女性 F => CC
-
-
大学 U
-
男性M => DD
-
女性 F => DD
-
-
-
年满50岁以上 L
-
研究生 G
-
男性 M => CC
-
女性 F => FF
-
-
大学 U
-
男性 M => EE
-
女性 F => FF
-
-
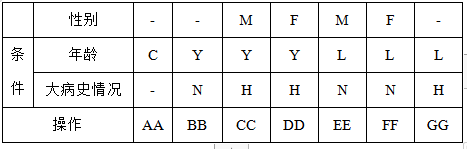
合并后得出如下判定表
“……对军人、残疾人或70岁以上的老人,应给予优先的业务处理……”这里假设“优先的业务处理”已在别处有更严格的定义,请建立判定表。
军人,残疾人,70岁以上老人分别代表了三种独立的状态,共有222=8种不同的组合
一一列出后合并便可得到如下判定表
功能描述:输入框的输入内容要求为数字或字母,长度要求为最短6个字符,最长20个字符。请用等价类划分和边界值分析相结合来设计测试用例。
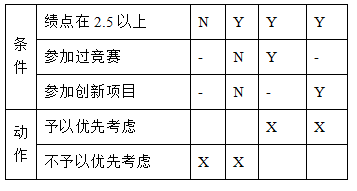
“……对成绩积点在2.5以上,并且参加过竞赛或创新项目的同学,在各类奖励中应给予优先考虑……”请建立判定表。
可以得出逻辑表达式如下:
予以考虑=(绩点在2.5以上) & (参加过竞赛 | 参加过创新项目)
得出真值表如下
| 绩点在2.5以上 | 参加过竞赛 | 参加过创新项目 | 予以优先考虑 |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
建立判定表如下
某保险公司对客户制定收费标准(标准等级用AA-GG表示),标准如下:
-
如果年龄不满18岁,不分男女性,标准为AA;如果年满18但不足50岁,大病例史为无,不分男女,标准BB;
-
如果年满18但不足50岁,大病例史为有,若是男性,标准为CC,若是女性,标准为DD;
-
如果年满50岁以上,大病例史为无,若是男性,标准为EE,若是女性,标准为FF;
-
如果年满50岁以上,大病例史为有,不分男女,标准为GG。
请对以上说明绘制判定表。为了便于绘制,条件符号使用以下内容:
-
不满18岁 C => AA
-
年满18但不足50 Y
-
无大病 N => BB
-
有大病 H
-
男性 M => CC
-
女性 F => DD
-
-
-
年满50 L
-
无大病 N
-
男性 M => EE
-
女性 F => FF
-
-
有大病 H => GG
-
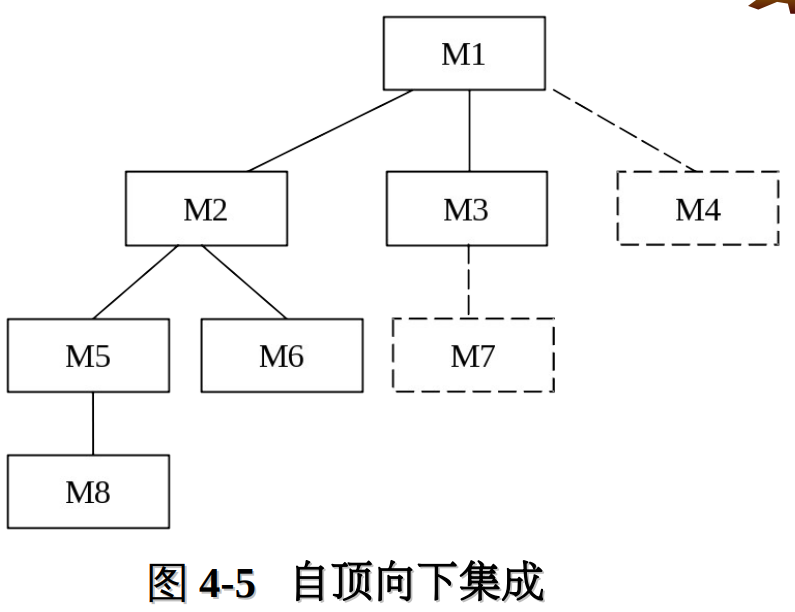
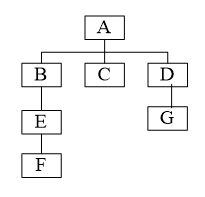
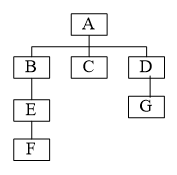
程序结构图如下图所示,请画出自顶向下集成的过程
自顶向下集成过程如下图所示
Si为相应的桩模块,用来模拟子模块
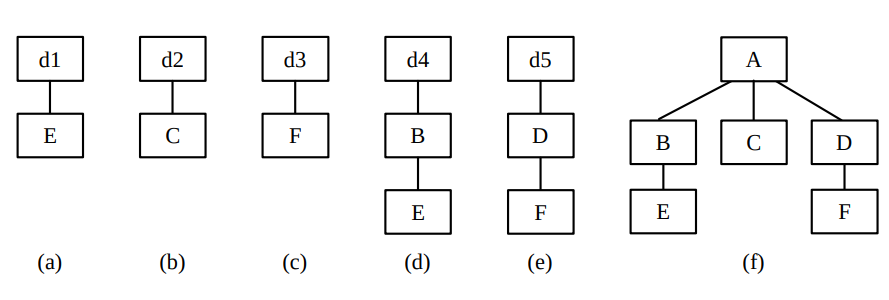
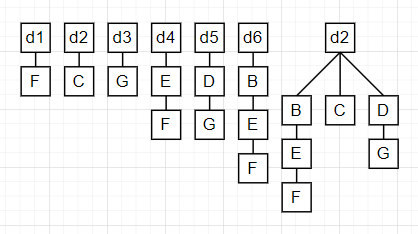
程序结构图如下图所示,请画出自底向上集成的过程
自底向上集成过程
di为子模块的驱动模块
需求描述如下:“输入三个整数a、b、c,分别作为三边的边长构成三角形。”通过程序判定所构成的三角形的类型,当此三角形为一般三角形、等腰三角形及等边三角形时,用等价类划分方法为该程序进行测试用例设计。
有一个处理单价为1元5角的盒装饮料的自动售货机软件,
-
若投入1元5角硬币,按下“可乐”、“雪碧”或“红茶”按钮,相应的饮料就送出来。
-
若投入的是2元硬币,在送出饮料的同时退换5角硬币,
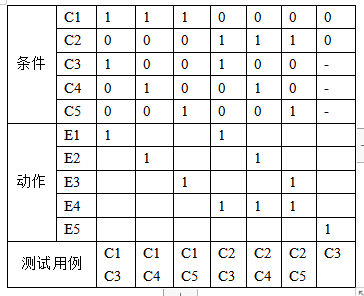
试用因果图法设计测试用例。
设有以下原因
- C1: 投入1.5元硬币
- C2: 投入2元硬币
- C3: 按下“可乐”
- C4: 按下“雪碧”
- C5: 按下“红茶”
设有以下结果
- E1: 送出可乐
- E2: 送出雪碧
- E3: 送出红茶
- E4: 退还5角硬币
- E5: 不送出任何东西
解题如下
-
若投入1.5元硬币 C1
-
按可乐C3=>E1
-
按雪碧C4=>E2
-
按红茶C5=>E3
-
-
若投入2元硬币 C2
-
按可乐C3=>E1 E4
-
按雪碧C4=>E2 E4
-
按红茶C5=>E3 E4
-
手机号码验证的描述如下:
-
输入的内容必须是数字,并且位数为11位,满足以上情况显示输入正确;
-
如果输入内容有非数字,则显示内容有误;
-
如果输入位数不为11位,则显示位数有误。
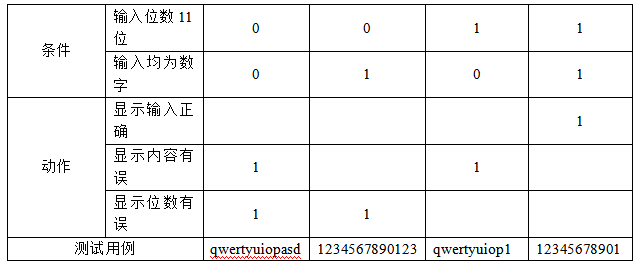
请用因果图法设计测试用例。
-
输入位数为11位
-
输入为数字
- 显示输入正确
-
输入有非数字
- 显示内容有误
-
-
输入位数不为11位
- 显示位数有误