图形学-Geometry几何

Geometry 几何

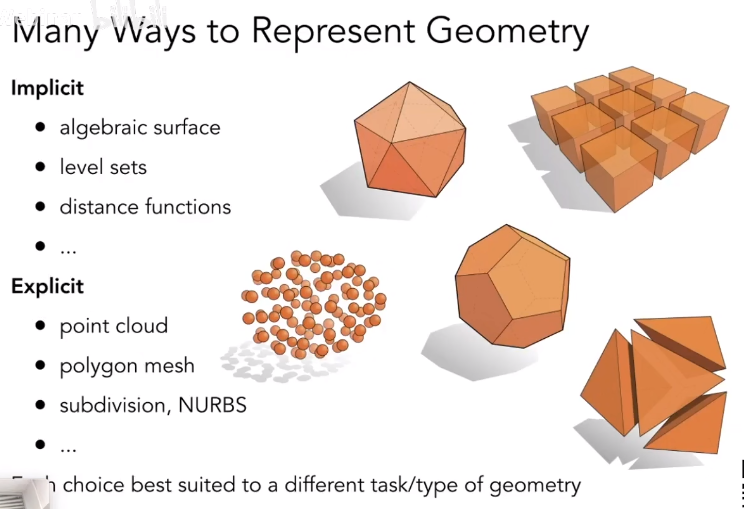
表达几何的方式有很多种，基本可以分为两大类：

• 隐式表示
  • Algebraic Surface 代数曲面
  • Level Set 水平集
  • Distance Function 距离函数
    • Signed Distance Function(SDF): 有符号距离函数
    • Unsigned Distance Function(UDF): 无符号距离函数
  • …
• 显式表示
  • Point Cloud 点云
  • Polygon Mesh 多边形网格
  • subdivision, NURBS
  • …

几何的表示方式

几何的隐式表示

隐式不会告诉具体的点在哪，只描述点满足什么约束关系，如对于一个球的隐式表示如下：

$x^2 + y^2 + z^2 = r^2$

更通用的表述方式为满足$f(x, y, z) = 0$的点集，就可以描述一个隐式的几何表示。

隐式表示的缺点是不直观并不知道有哪些点，优点是很轻易可以判断一个点是否在几何上，几何内还是几何外。

基于代数方法的隐式表示

使用代数方程来描述几何体

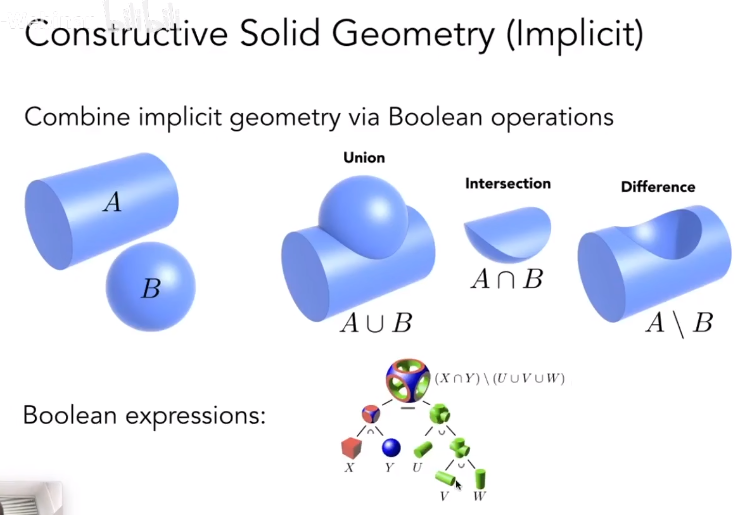
CSG(Constructive Solid Geometry) 构造实体几何

通过布尔运算来构造复杂的几何体

Distance Function 距离函数

空间中的一个点，到物体表面上的最小距离的距离函数可以隐式地表示一个几何体

对两个几何体使用 SDF 表示，并通过 blend 操作，可以逐渐地将两个几何体融合在一起

Level Set 水平集

和 SDF 类似，只不过水平集使用了数值描述 SDF 函数。

Fractals 分形

几何的显式表示

所有的点都直接给出或者通过参数化映射的方式给出。

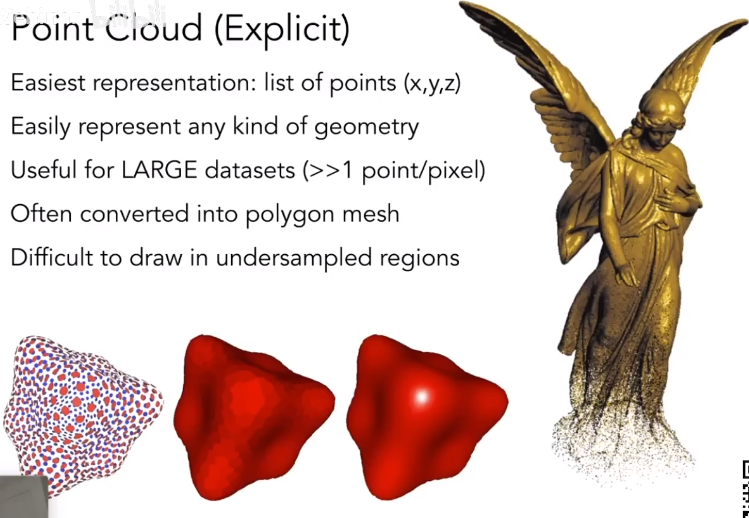
Point Cloud 点云

一般由激光扫描仪等设备采集得到。

可以通过点云重建算法将点云转换为多边形网格。

Polygon Mesh 多边形网格

这种方式几乎是目前图形学中最广泛使用的几何表示方式。

如 obj 文件格式

其中描述了物体的一堆顶点，每个顶点的法线和纹理坐标，以及每个面由哪些顶点组成。

曲线与曲面

Bézier Curve 贝塞尔曲线

使用起始点，终止点和一系列控制点来定义一条曲线。

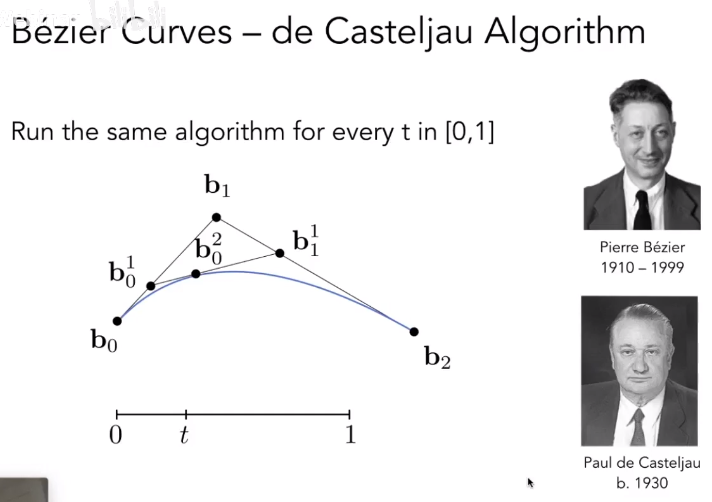
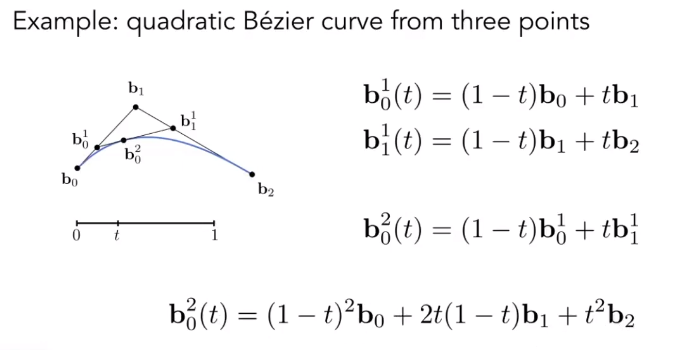
二次贝塞尔曲线

如图起始点为$b_0$，终止点为$b_2$，控制点为$b_1$。

有一个参数$t \in [0, 1]$，当$t=0$时曲线在起始点，当$t=1$时曲线在终止点。

$b_0^1$为$b_0$和$b_1$之间的线性插值，$b_0^1$将直线$b_0 b_1$按比例 t 分割。

$b_1^1$为$b_1$和$b_2$之间的线性插值，$b_1^1$将直线$b_1 b_2$按比例 t 分割。

曲线上的点$b_0^2$为$b_0^1$和$b_1^1$之间的线性插值，$b_0^2$将直线$b_0^1 b_1^1$按比例 t 分割。

最终$b_0^2$即为曲线上的点。

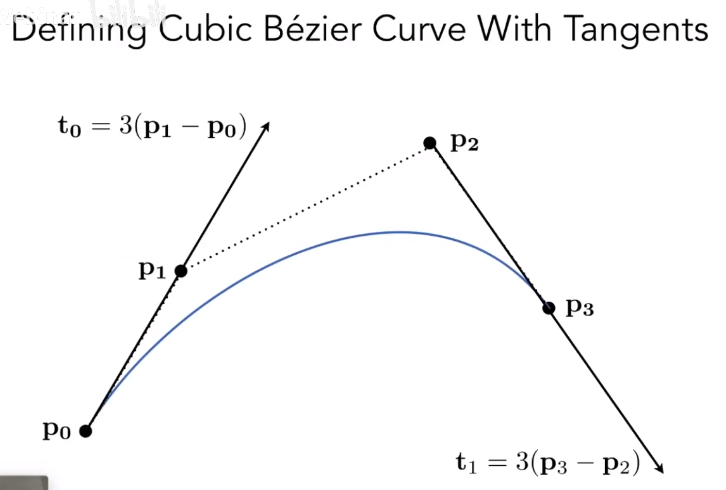
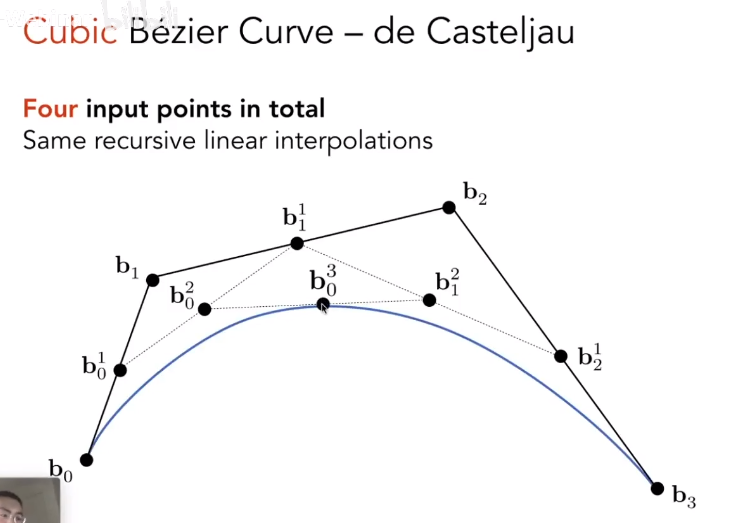
三次贝塞尔曲线

如图起始点为$b_0$，终止点为$b_3$，控制点为$b_1$和$b_2$。

有一个参数$t \in [0, 1]$，当$t=0$时曲线在起始点，当$t=1$时曲线在终止点。

$b_0^1$为$b_0$和$b_1$之间的线性插值，$b_0^1$将直线$b_0 b_1$按比例 t 分割。

$b_1^1$为$b_1$和$b_2$之间的线性插值，$b_1^1$将直线$b_1 b_2$按比例 t 分割。

$b_2^1$为$b_2$和$b_3$之间的线性插值，$b_2^1$将直线$b_2 b_3$按比例 t 分割。

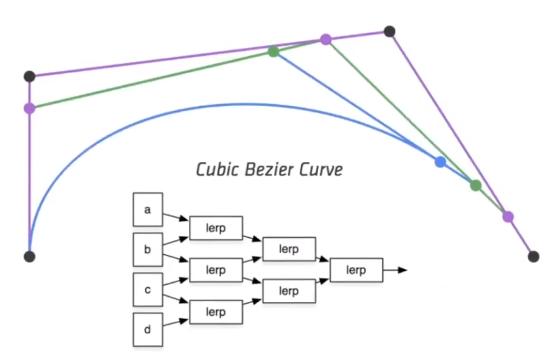
最后问题规模减小为二次贝塞尔曲线，继续按照二次贝塞尔曲线的上面的方式计算即可。

实际上是一个递归的过程。

n 次贝塞尔曲线

对于给定的$n+1$个点$b_0, b_1, \ldots, b_n$，可以定义出 n 次贝塞尔曲线的公式：

$b^n(t) = \sum_{j=0}^{n} b_j \cdot B_j^n(t)$

$b^n(t)$为曲线上的控制点

$b_j$为第 j 个控制点

$B_j^n(t)$为伯恩斯坦多项式，定义为：

$B_j^n(t) = C_n^j \cdot t^j \cdot (1-t)^{n-j}$

贝塞尔曲线的性质

• 一定经过起点和终点 $b^n(0) = b_0, b^n(1) = b_n$
• 贝塞尔曲线的仿射不变性：如果对所有控制点进行仿射变换，则曲线也会进行相同的仿射变换。
• 凸包性质：
  • 贝塞尔曲线的所有点都在控制点的凸包内。
  • 如果所有控制点都在同一条直线上，则贝塞尔曲线也在这条直线上。

分段贝塞尔曲线

当控制点太多时候，很难控制曲线，可以将曲线分成多个段，每个段使用一个贝塞尔曲线来表示。

一般常用的是三次贝塞尔曲线。

样条曲线

使用一系列的必经点来定义一条曲线。

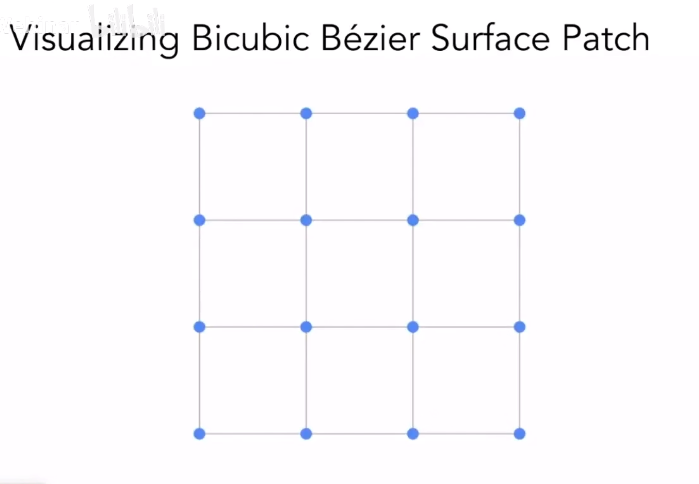
贝塞尔曲面

将贝塞尔曲线推广到三维空间中，可以得到贝塞尔曲面。

贝塞尔曲面的推广类似于双线性插值的思想。

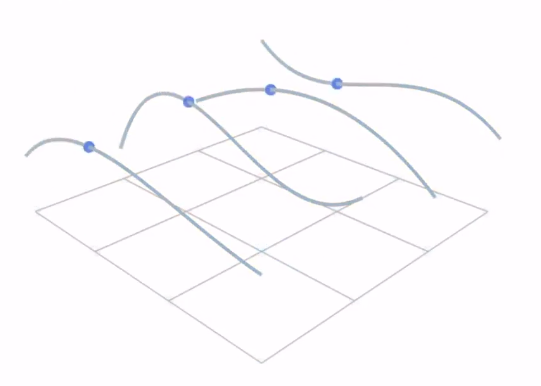
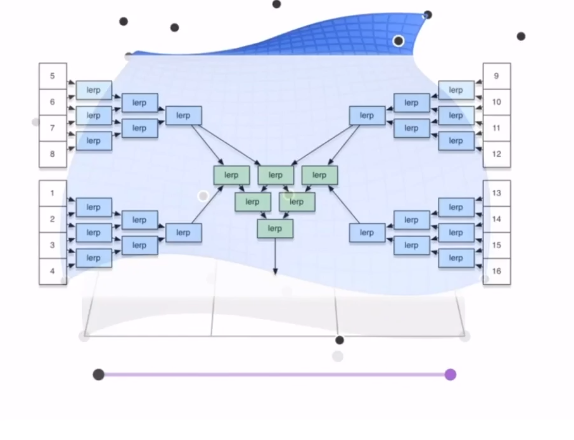
如图有 16 个控制点

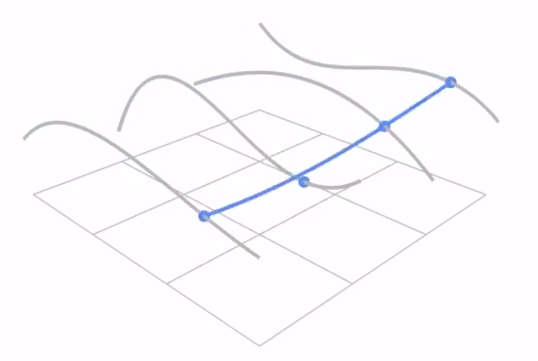
水平方向是随着 t 的变化，可以绘制出四条贝塞尔曲线，将这四个曲线上对应 t 时刻的点再认为是另外一个贝塞尔曲线的控制点，则可以再得到一个贝塞尔曲线。

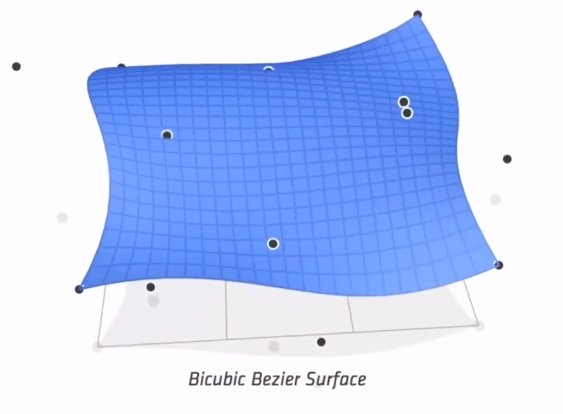
最终得到了一个贝塞尔曲面。