单质点模拟
首先,提出先聚焦于单个粒子的运动,之后再将研究推广到大量粒子的情况。
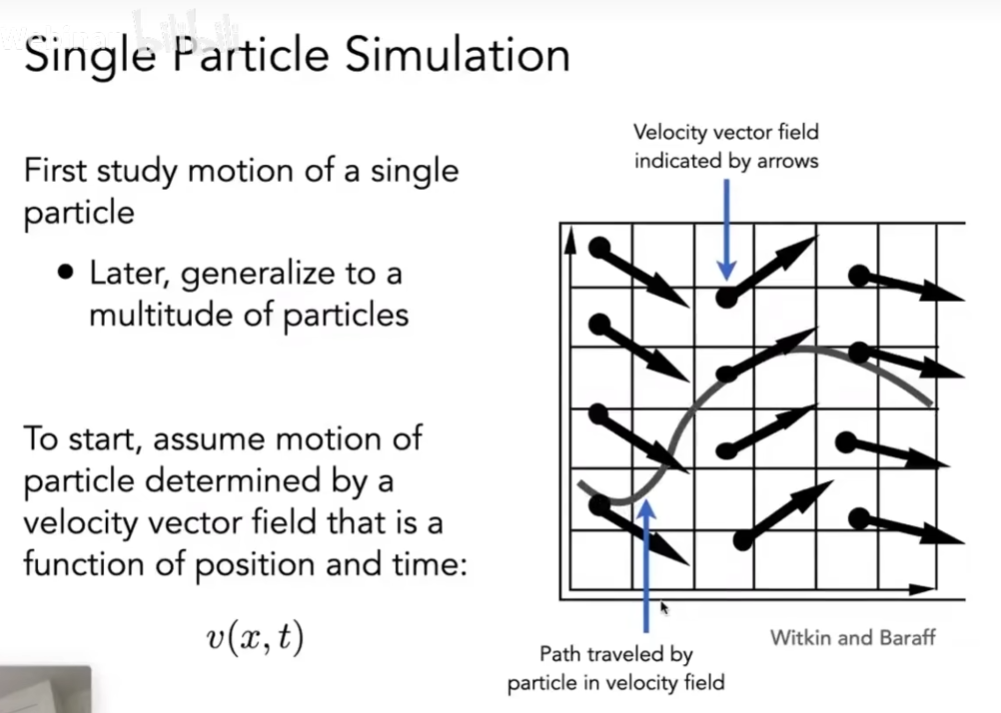
为开展研究,假设粒子的运动由速度矢量场决定。该速度矢量场是位置和时间的函数,记为。
右侧的图示直观呈现了速度矢量场(由箭头表示)以及粒子在该速度场中运动的轨迹。
常微分方程 Ordinary Differential Equation (ODE)
计算速度场内粒子的位置需要计算一阶常微分方程
欧拉方法 Euler’s Method
欧拉方法,又称为前向欧拉,显式欧拉,是数值积分中最简单的方法之一。
- 使用很简单的迭代的方式
- 很常见
- 很不准
- 结果通常不稳定
始终使用前一段的量估计下一帧的量。
稳定性分析
这个方法存在两个关键问题:
- 时间步长 增大时,不准确性会随之增加
- 不稳定性是常见且严重的问题,可能导致模拟发散,右侧图形也直观展现了这种不稳定带来的模拟轨迹异常等情况,原先稳定的圆周运动逐步偏离了运动轨迹。
误差与不稳定性总结
通过有限差分进行数值积分求解通常会产生两个问题:
- 误差
- 每个时间步的误差会累积,随着模拟的推进,精度会下降。
- 在图形应用中,精度可能并非关键因素。
- 不稳定性
- 误差会叠加,即便底层系统本身不会发散,也会导致模拟发散。
- 缺乏稳定性是模拟中的一个根本性问题,不容忽视。
为了应对不稳定的问题,提供了一些其他方法:
- 中点法(改进的欧拉方法)
- 对起点终点速度取平均值
- 自适应步长法
- 递归比较一步和两个半步,直到误差可接受
- 隐式欧拉方法
- 使用下一步的量来估计下一步的量
- 需要解方程组
- 更稳定
- 难度大
- 基于位置的/Verlet 积分法
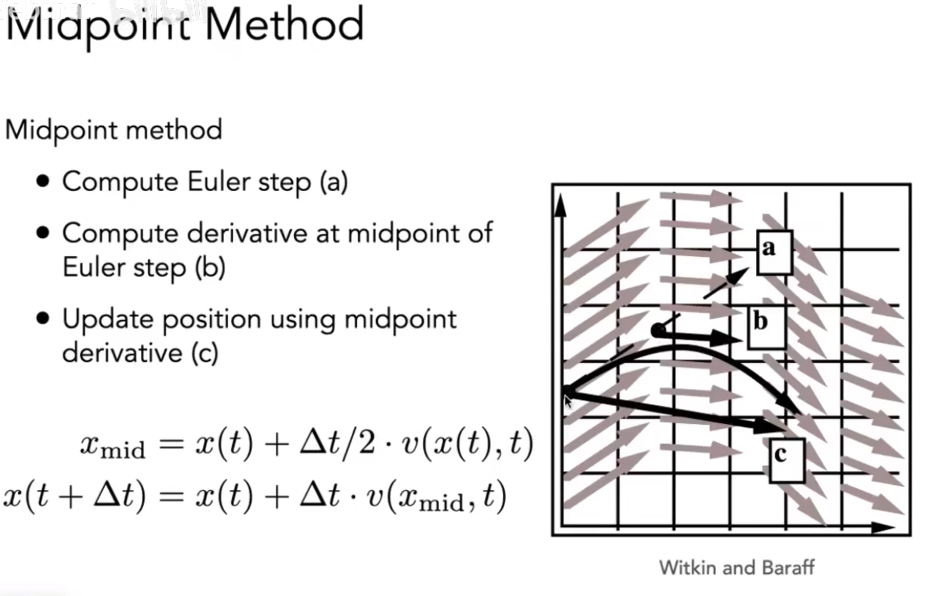
中点法 Midpoint Method
中点法:
- 先用欧拉法计算出下一个位置
- 再计算出中点的位置
- 最后用中点的速度作为下一帧的速度来更新位置得到最终的位置
改进的欧拉方法
中点法也称为改进的欧拉方法
使用上一时刻和下一时刻的速度的平均值来作为下一时刻的位置更新。
本质上和取上一时刻和下一时刻位置的中点的速度作为下一时刻的速度是一样的。
因为在一个时间步内,速度变化是线性的。所以中点速度就是上下时刻速度的平均值。
本质上是使用了二次项来提高精度。
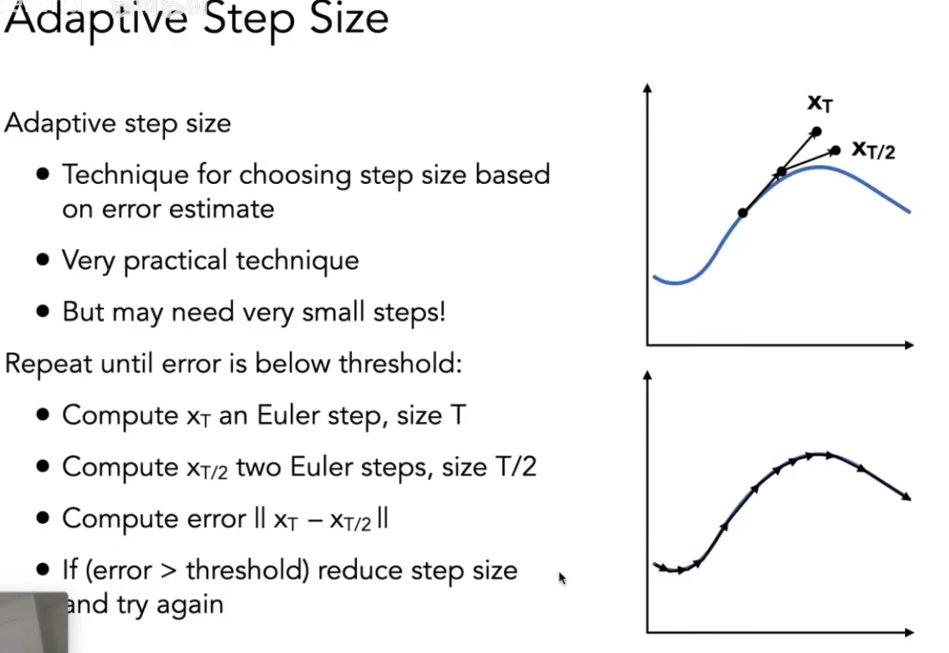
自适应步长
- 是一种基于误差估计来选择步长的技术。
- 是非常实用的技术,但可能需要非常小的步长!
重复操作直到误差低于阈值:
- 计算步长为 $ T $ 的欧拉步 $ x_T $。
- 计算两步步长为 $ T/2 $ 的欧拉步 $ x_{T/2} $。
- 计算误差 $ | xT - x{T/2} | $。
- 如果(误差 > 阈值),则减小步长并再次尝试。
隐式欧拉方法 Implicit Euler’s Method
隐式欧拉法:
- 隐式方法:
- 通俗称为后向方法。
- 为当前步计算,会用到未来的导数。
- 公式:
- $ \boldsymbol{x}^{t + \Delta t} = \boldsymbol{x}^t + \Delta t \dot{\boldsymbol{x}}^{t + \Delta t} $
- $ \dot{\boldsymbol{x}}^{t + \Delta t} = \dot{\boldsymbol{x}}^t + \Delta t \ddot{\boldsymbol{x}}^{t + \Delta t} $
- 要为 $ \boldsymbol{x}^{t + \Delta t} $ 和 $ \dot{\boldsymbol{x}}^{t + \Delta t} $ 求解非线性问题。
- 采用求根算法,比如牛顿法。
- 具备好得多的稳定性。
稳定性的定义
如何确定/量化“稳定性”?
-
我们使用局部截断误差(每一步)/总累积误差(整体)。
-
误差的绝对值不重要,但与步长相关的阶数很重要。
-
隐式欧拉法是 1 阶的,这意味着:
- 局部截断误差:$ O(h^2) $
- 全局截断误差:$ O(h) h $ 是步长,即 $ \Delta t $)
-
对 $ O(h) $ 的理解:
- 如果我们将 $ h $ 减半,我们可以预期误差也会减半。
龙格-库塔方法 Runge-Kutta Families
龙格 - 库塔(Runge - Kutta)方法族:
是一类用于求解常微分方程(ODEs)的高级方法。
- 尤其擅长处理非线性问题。
- 其四阶版本(常称 RK4)是使用最广泛的。
初始条件:
,。
RK4 求解公式:
其中:
基于位置的 / 韦尔莱(Verlet)积分
核心思想:
- 在改进的欧拉前向步计算后,约束粒子的位置,以防止出现发散、不稳定的行为。
- 利用受约束的位置来计算速度。
- 这两种思路都会消耗能量,可能不太符合能量守恒,从而实现最终稳定。
优缺点:
- 快速且简单。
- 不符合物理实际,会消耗能量(带来误差)。
细节见作业 8。
刚体模拟(Rigid Body Simulation)
- 由于刚体不会发生形变,故和粒子模拟类似。
- 只是需要考虑更多属性。
数学模型
符号说明
- $ X $:位置
- $ \theta $:旋转角度
- $ \omega $:角速度
- $ F $:力
- $ \Gamma $:力矩
- $ I $:转动惯量
流体模拟
一种简单的基于位置的方法
核心思想
- 假设水由小的刚体球体组成。
- 假设水不可压缩(即密度恒定)。
- 因此,只要某处密度发生变化,就应通过改变粒子的位置来“修正”。
- 需知道密度相对于每个粒子位置的梯度。
- 更新方式?只需用梯度下降法!
(右侧图片来源:[Macklin et al.])
欧拉法与拉格朗日法(Eulerian vs. Lagrangian)
是模拟大量物质集合的两种不同视角。
拉格朗日法(Lagrangian Approach,“质点法”)
摄影师全程跟随同一只鸟,追踪其运动轨迹。
欧拉法(Eulerian Approach,“网格法”)
摄影师保持静止,仅拍摄在某个时刻(比如时刻 $ t $)经过某一画面的所有鸟。
(参考视频:https://www.youtube.com/watch?v=IDlzlkic1pY)
物质点法(Material Point Method, MPM)
是结合欧拉法和拉格朗日法视角的混合方法:
- 拉格朗日视角:考虑携带材料属性的粒子。
- 欧拉视角:使用网格进行数值积分。
- 交互过程:粒子将属性传递给网格,网格执行更新,然后再插值回粒子。
(右侧图片来源:[Stomakhin et al. 2014],©Disney)