- 动画是一种信息传递的工具
- 美学经常比技术重要
- 是模型的延伸 → 连续性
- 将场景模型表示为时间的函数
- 输出一系列图像,当顺序查看时提供运动的感觉
- 帧率
- 电影:24FPS
- 视频:30FPS、29.994FPS
- VR:90FPS (不晕的基础要求)
关键帧动画
- 动画师创建关键帧
- 助手(人工或程序)创建中间帧
其中的关键技术即为插值技术
- 线性插值: 通常可能不太满足动画需求
- 样条插值: 更平滑的插值方式
- Catmull-Rom 样条
- B 样条
- Bezier 曲线
物理仿真动画
模拟、仿真:推导、实现公式,模拟出物体应该怎么变化
例子:布料模拟、流体模拟
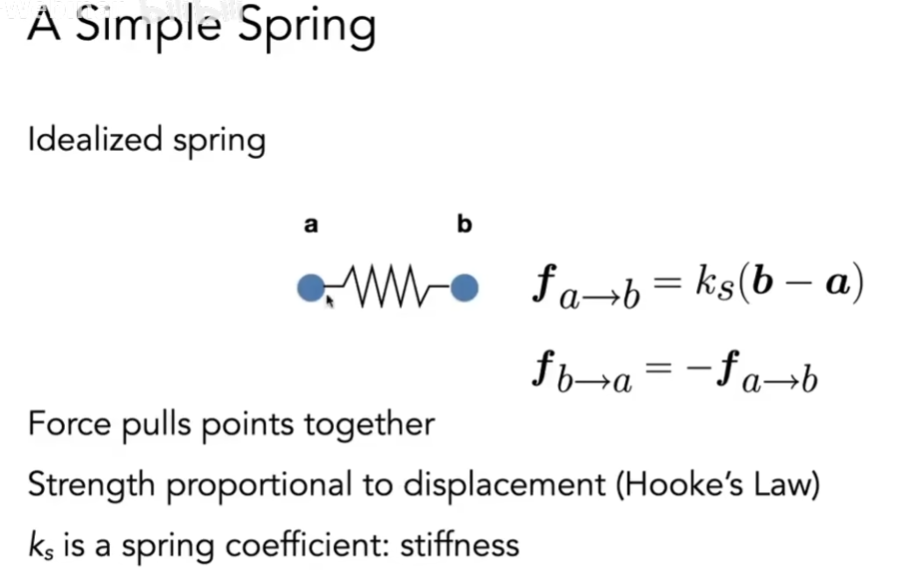
质点弹簧系统 Mass-Spring System
一个弹簧左右连接两个质点,位置是,弹簧劲度系数为。
当弹簧拉伸时候,弹簧会对两个质点施加一个拉力:
质点受到的往方向的拉力为:
质点受到的往方向的拉力为:
这就是胡克定律。
非零长度的弹簧
但是实际的弹簧不可能是零长度的,假设弹簧的自然长度为,称之为rest length则弹簧拉力变为:
公式表达了:
- 当弹簧被拉伸时,,即弹簧拉伸了多长的长度,再带上弹簧的劲度系数,再乘上一个单位方向向量受力方向,得到弹簧对质点的拉力的向量。
- 当弹簧被压缩时,,即弹簧压缩了多长的长度,再带上弹簧的劲度系数,再乘上一个单位方向向量受力方向,得到弹簧对质点的推力的向量。
带阻尼的弹簧
但是只按照上面的弹簧力来模拟的话,弹簧会一直振动下去,永远不会停下来。因为能量守恒导致其中的动能和势能会一直在相互转换。
导数记号
在物理仿真中,常用记法:
- 使用表示一个位置向量。
- 使用表示位置向量的时间导数,即速度向量。
- 使用表示位置向量的二阶时间导数,即加速度向量。
Damping Force 阻尼力
这里可以引入阻尼力,假设一个质点受到的阻尼力与其速度成正比,且方向总是与速度相反:
其中为阻尼系数。这将会让质点的速度逐渐变小,最终停下来。
问题:这将会让所有的运动都停下来。假设弹簧相连的两个质点相对静止,但整体在运动,这时阻尼力就会让整体运动都停下来。
弹簧的内部阻尼力
考虑到以下思考:
- 弹簧的阻尼力只是一个弹簧系统的内力
- 弹簧的对质点的阻尼力只与两个质点的相对速度有关,与其整体的速度无关
- 弹簧对质点的阻尼力只与沿着弹簧方向上的速度有关,假如 b 绕 a 做匀速圆周运动,则弹簧的长度不变,弹簧不应该对质点施加阻尼任何力
假设弹簧连接的两个质点,则弹簧对质点的阻尼力为:
为质点指向质点的单位方向向量。
为质点相对于质点在弹簧方向上的相对速度的大小。
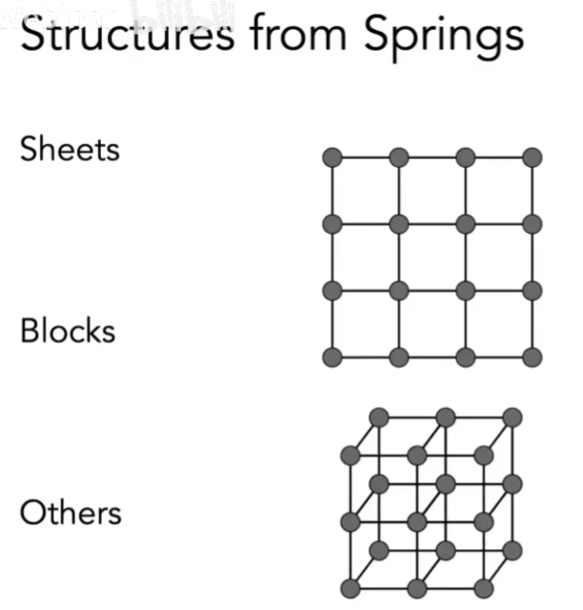
弹簧结构
使用质点弹簧系统可以组合出各自各样的结构。
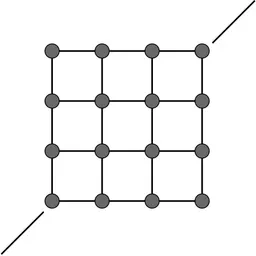
使用质点弹簧系统仿真一块布
此时如果沿着副对角线拉伸,则主对角线方向会轻易被压缩成一条线。不符合实际情况。
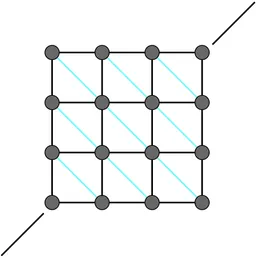
对主对角线方向上添加弹簧,当布料被拉伸时,主对角线方向的弹簧会被压缩,产生一个推力来抵抗布料被压缩。但它此时并不对称。
继续对副对角线方向上添加弹簧,布料就会比较稳定。
但对于三维空间中,布料发生折叠时,无法表现出抗折叠的效果。
继续在每隔一个质点之间添加弹簧,布料就会比较稳定。
有限元方法 Finite Element Method (FEM)
基于力传导扩散的物理仿真方法
粒子系统 Particle System
- 将动态系统建模为大量粒子的集合
- 每个粒子的运动由一组物理(或非物理)力定义
- 是图形学和游戏领域的流行技术
- 易于理解和实现
- 可扩展:少粒子追求速度,多粒子提升复杂度
- 挑战
- 可能需要大量粒子(例如流体模拟)
- 可能需要加速结构(例如为了查找交互所需的最近粒子)
粒子系统的基本算法
对于每一个动画帧
- [Optional] 创建新的粒子
- 计算每个粒子所受的力
- 更新每个粒子的速度和位置
- [Optional] 删除不需要的粒子
- 渲染所有粒子
粒子系统的力
吸引力和排斥力
- 重力、电磁力等
- 弹簧力、推进力等
阻尼力
- 摩擦力、空气阻力、粘性力等
碰撞
- 墙壁、容器、固定物体等
- 动态物体、角色身体部位等
万有引力
牛顿万有引力定律,粒子之间会受到吸引力,
为万有引力常数
星系模拟
流体模拟
作为常微分方程(ODE)的模拟鸟群的运动
将每只鸟建模为一个粒子,使其受到非常简单的力:
- 对邻居中心的吸引力
- 来自单个邻居的排斥力
- 朝着邻居平均运动轨迹的对齐力
对大型粒子系统的演化进行数值模拟,会出现涌现的复杂行为(在鱼类、蜜蜂等生物中也能看到)。
http://www.red3d.com/cwr/boids/
分子运动模拟
正运动学
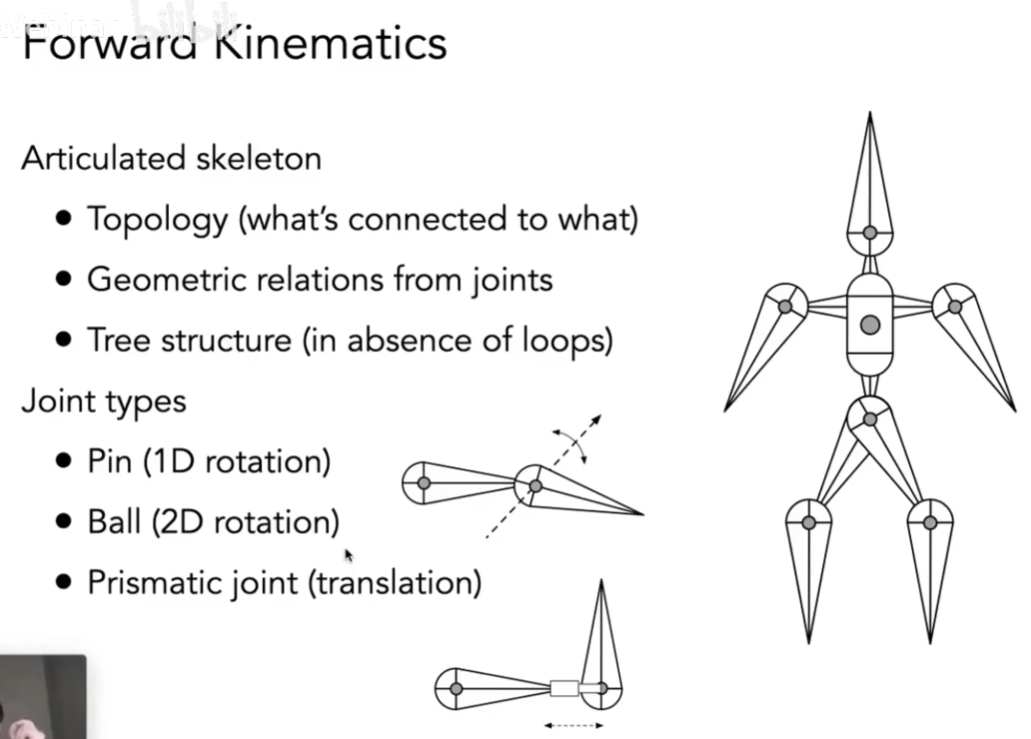
可以定义一个骨骼系统
- 拓扑(如何连接)
- 关节的位置
- 树结构,可以用来加速求解
关节类型:
- Pin (只能围绕一个点在平面内旋转)
- Ball (可以围绕一个点在空间上任意旋转)
- Prismtic joint (可以围绕一个轴线平移)
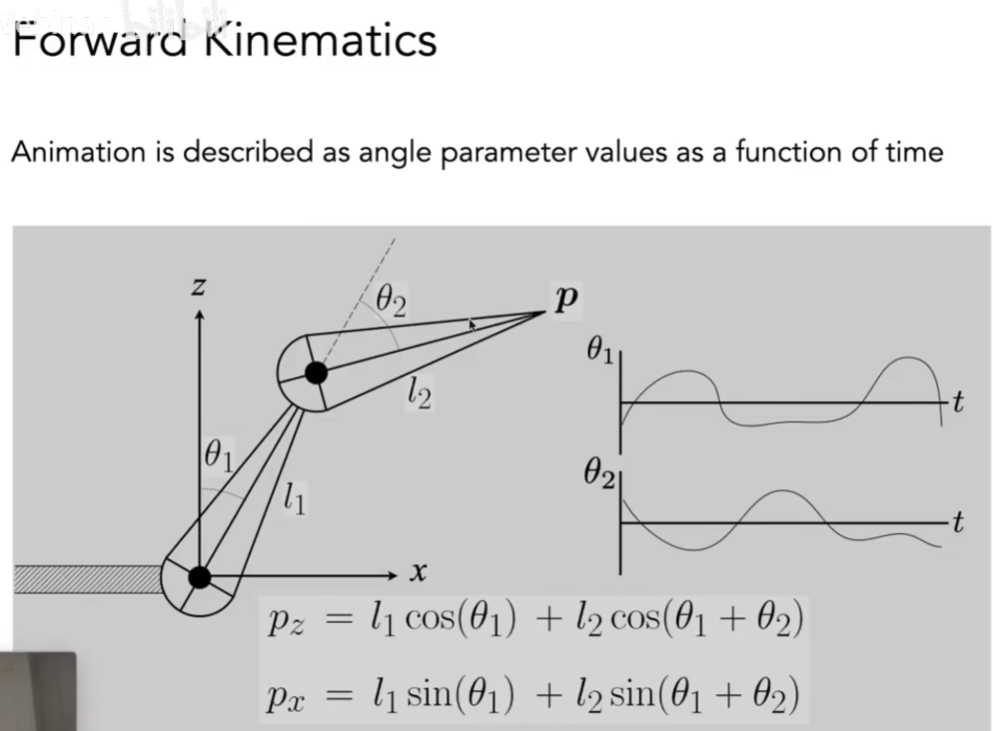
如图是模拟了一个 2D 的手臂,包含大臂和小臂两个部分。
最终末端的位置为:
正向运动学
动画被描述为角度参数值随时间变化的函数。
同时如果角度 $ \theta_1,\theta_2 $ 随时间 t 变化,则也可以计算出尖端位置随时间的变化。
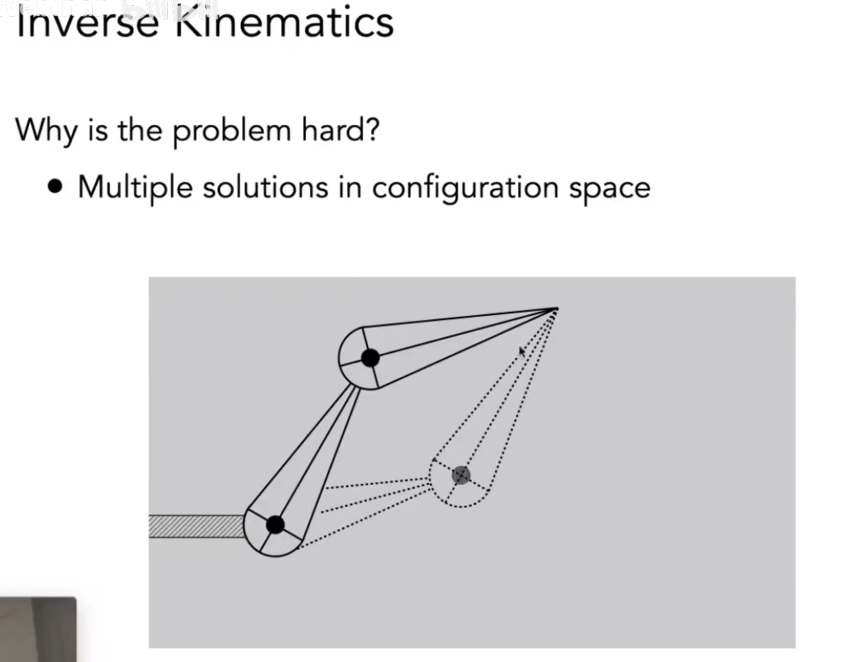
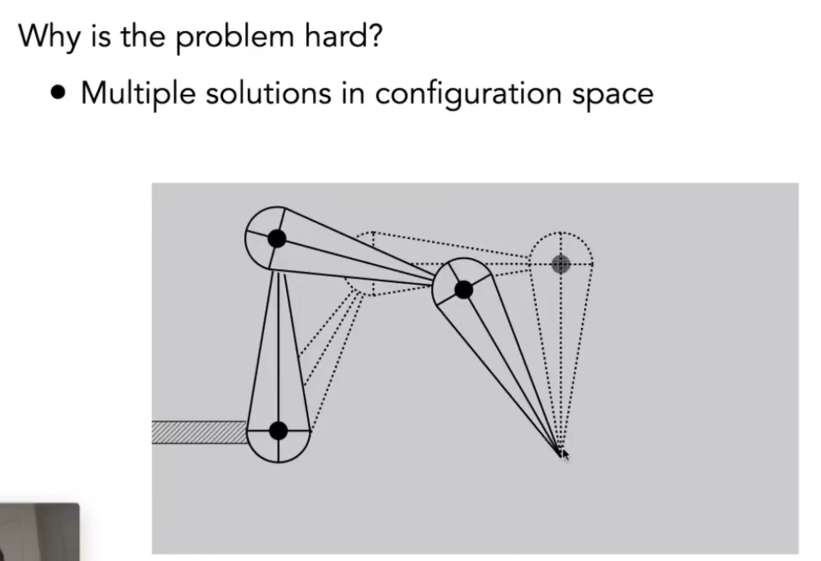
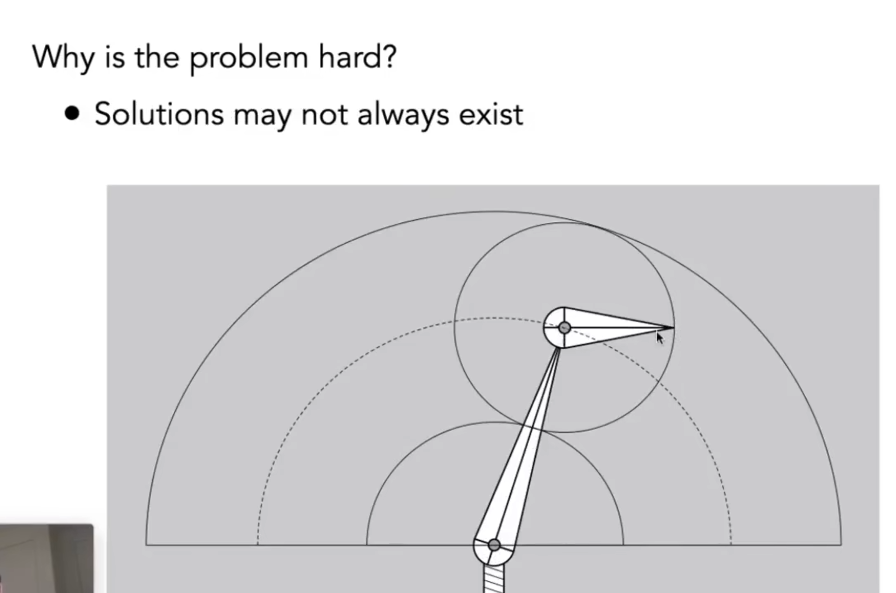
逆运动学
直接逆运动学:如图给两端手臂,可以直接求出其解析解。
可能会出现多解和无解的问题。
数值逆运动学:对于复杂的骨骼系统,无法直接求出解析解,可以使用优化方式来求解,如梯度下降法求解出各个关节的参数使得末端位置尽可能接近目标位置。
Rigging 绑定
绑定是对角色的一组更高级别的控制,能更快速、直观地修改姿势、变形、表情等。
重要点:
- 就像木偶上的线
- 涵盖角色所有有意义的变化
- 因角色而异
说白了即添加各种控制点可以通过控制点来控制角色的各种动作。
动作捕捉
通过传感器捕捉真实人的控制点的变化,反映到虚拟角色上的控制点的变化。
动作捕捉技术有优势也存在不足。优势在于能快速捕捉大量真实数据,且能实现较高的真实感;不足则是设备安装复杂且成本高,同时捕捉到的动画可能不符合艺术需求,需要进行修改。
光学动捕
实际使用中,这种方式较为广泛应用
- 人身上贴一些标签
- 各个位置摆放很多摄像头
- 需要高速相机,至少 240Hz 来捕获变化