图形学-Sharding着色

Sharding 着色

图形学中 Sharding 的概念值对一个物体应用不同的材质的过程。

光照 Lighting

Blinn-Phong 反射模型(BPR)

Blinn-Phong 反射模型是对光线与物体表面交互的一个经验模型。

它将光线与物体表面的交互分为三个部分：

• 环境光：物体表面在没有直接光照的情况下的颜色
• 漫反射：物体表面在直接光照下的颜色，取决于光源的颜色和物体表面的颜色
• 高光反射：物体表面在直接光照下的高光部分，取决于光源的颜色、物体表面的颜色和观察者的视角

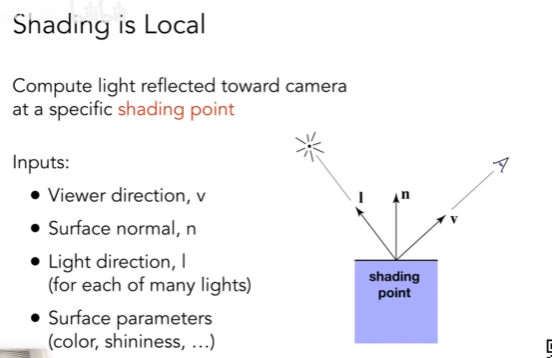
计算光线从一个着色点反射到相机中中的颜色：

输入变量定义如下：

• $v$: 观察者的视角的单位向量
• $l$: 表示光源的方向的单位向量
• $n$: 物体表面着色点的单位法向量
• 表面材质（颜色，反光程度，…）

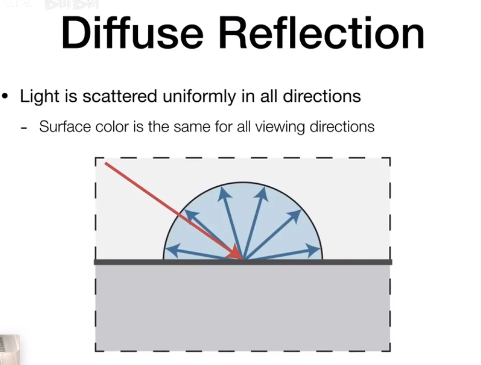
漫反射

一根光线从光源发出，照射到着色点后，会沿四周反射，即为漫反射。

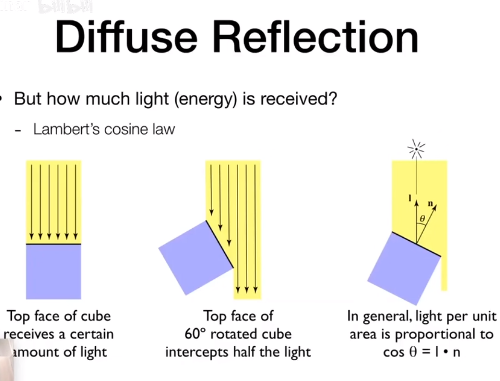
Lambert’s Cosine Law 描述了漫反射的强度与光线入射角的关系。

当光线垂直入射时，物体表面几乎可以接收到全部的光线能量。
当光线倾斜入射时，物体表面接收到的光线能量会减少。
当光线平行于物体表面时，物体表面几乎无法接收到光线能量。

设光线方向向量为 $l$，着色点的法向量为 $n$，它们的夹角余弦为$\cos \theta = l \cdot n$。

• $\theta$越小，$\cos \theta$越大，光线越直射，漫反射强度越大
• $\theta$越大，$\cos \theta$越小，光线越平行，漫反射强度越小

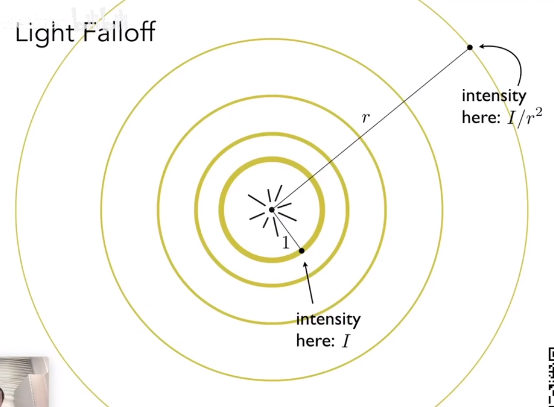
对于一个点光源，可以看作是沿着球面向四周均匀辐射能量，同样遵循平方反比定律。

设$I_0$为光源的强度，$r$为光源到着色点的距离，则光线到达着色点的强度为：

$I_l = \frac{I_0}{r^2}$

则可以得到最终的漫反射光照强度：

$L_d = k_d \cdot I(r) \cdot \max(0, cos \theta) = k_d \cdot \frac{I_0}{r^2} \cdot \max(0, l \cdot n)$

$k_d$ 是物体表面的漫反射系数，取值范围为$[0,1]$，表示物体表面对漫反射光的吸收能力。

• $k_d = 0$ 时，物体表面对漫反射光完全吸收，漫反射光照强度为 0
• $k_d = 1$ 时，物体表面对漫反射光完全反射，漫反射光照强度最大
• $k_d$ 越大，物体表面对漫反射光的吸收能力越弱，反射出去的漫反射光照强度越大
• $k_d$ 越小，物体表面对漫反射光的吸收能力越强，反射出去的漫反射光照强度越小

max(0, l · n) 的作用是确保漫反射光照强度不会为负值。当$\theta$大于 90 度时，光线与法向量的夹角为钝角，此时光线可能从物体内部发出，并没有什么物理意义，故直接取 0。

$I_0$ 是点光源的强度，通常是一个常数。

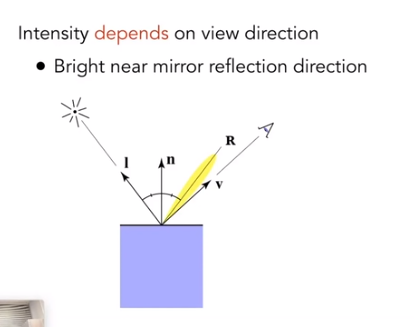
高光反射

当视线向量$v$足够接近于镜面反射方向$R$时，此时高光反射最为明显。

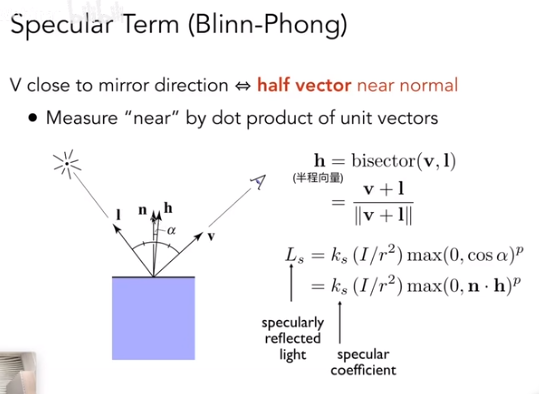
半程向量$h=bisector(v,l)=\frac{v+l}{||v+l||}$

而视线向量$v$足够接近于镜面反射方向$R$实际上又等价于半程向量$h$与法向量$n$足够接近，设 h 和 n 之间的夹角为 $\alpha$，则有：

$\cos \alpha = h \cdot n$

因此高光反射的强度可以表示为：

$L_s = k_s \cdot I(r) \cdot \max(0, \cos \alpha)^p = k_s \cdot \frac{I_0}{r^2} \cdot \max(0, h \cdot n)^p$

$K_s$ 是物体表面的高光反射系数，取值范围为 $[0,1]$。

$I(r)$ 是点光源的强度，通常是一个常数。

$p$ 是高光反射的衰减指数，通常取值范围为 $[0, 90\degree]$
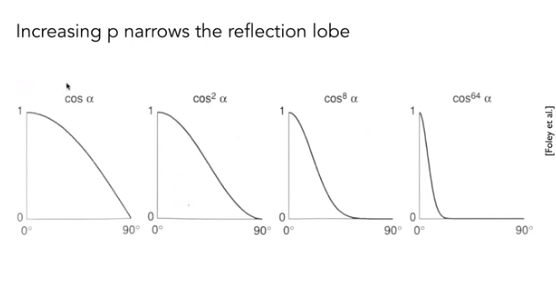
，表示高光反射的锐利程度，如下图为不同指数下的$cos^p \alpha$的衰减程度：

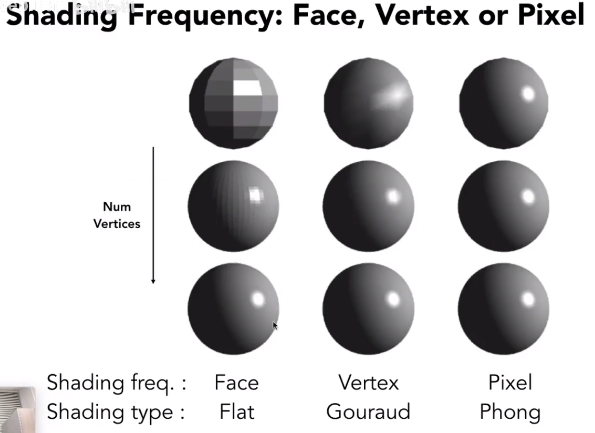
如图从上到下看，$K_s$越来越大，高光亮度越来越大。
从左到右看，$p$越来越大，高光反射的锐利程度越来越高（白色高光区域越来越集中）。

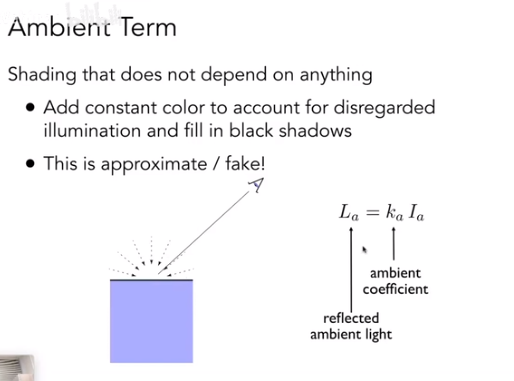
环境光

环境光实际上是一个非常简单的假设，我们假设环境光就是一个常数，在没有漫反射光和高光反射光的情况下，物体表面的颜色。

$L_a = k_a \cdot I_a$

$K_a$ 是物体表面的环境光系数，取值范围为 $[0,1]$。
$I_a$ 是环境光的强度，通常是一个常数。

PS: 如果需要精确计算环境光，则需要全局光照相关的知识，非常复杂。

最后将三种光照强度相加，得到最终的物体渲染结果的颜色：

$\begin{aligned} L &= L_d + L_s + L_a \\ &= k_d \cdot \frac{I_0}{r^2} \cdot \max(0, l \cdot n) + k_s \cdot \frac{I_0}{r^2} \cdot \max(0, h \cdot n)^p + k_a \cdot I_a \end{aligned}$

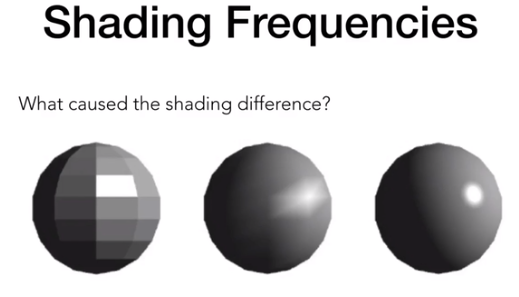
着色频率 Sharding Frequencies

从这三个球的边界可以看出，这三个球的模型是完全相同的，但最终看起来的结果各不相同，这是因为着色频率的不同而导致的结果。

• 第一个球是把着色应用在面上，一个三角面上只有一种单一颜色。
• 第二个球是把着色应用在了顶点上，每个顶点有一个颜色，三角面内的颜色通过顶点插值计算得到。
• 第三个球是把着色应用在了每一个像素上，每一个顶点有自己的法向量，三角面片中的每一个点都可以插值计算出自己的颜色和法向量，再对每一个像素点都进行一次着色计算。

着色模型

Flat Shading

Flat Shading 就是指先前的第一种着色模型，只应用在三角形的面上。

Gouraud Shading

Gouraud Shading 就是指先前的第二种着色模型，应用在三角形的顶点上。三角形内的颜色通过顶点插值计算得到。

Phong Shading

Phong Shading 就是指先前的第三种着色模型，应用在每一个像素上。每个顶点有自己的法向量，三角面片中的每一个点都可以插值计算出自己的颜色和法向量，再对每一个像素点都进行一次着色计算。

不同着色模型效果对比

当模型面片足够密集时，Flat Shading, Gouraud Shading 可能与 Phong Shading 的效果差不多，但计算量会减少很多，所以不同情况下可能会选择不同的着色模型。

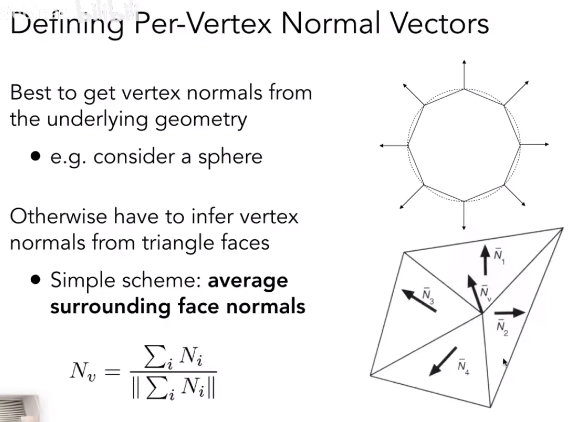
定义顶点法线

对于一个确定的几何形体，如一个球，法线方向则可以直接通过球心到顶点的向量计算得到。

对于一些不规则的三角面组成的几何形体，可以由顶点周围的三角面片平均来计算顶点的法线，为了更好地效果，也可以是加权平均得到，权重可以是三角面片的面积。

三角形内部的像素级法线

对于一个三角形的内部像素点，可以通过顶点的法线插值计算得到。

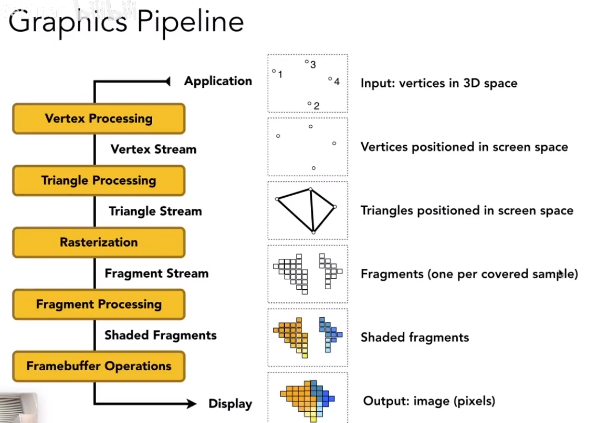
图形管线 Graphics Pipeline/实时渲染管线

图形管线就是将先前所有的渲染流程组合成一个完整的渲染流程：

• 顶点处理 Vertex Processing
  • 输入：三维空间中的顶点数据
  • 输出：已经映射到了屏幕空间中的顶点数据
• 三角形处理 Triangle Processing
  • 输入：上一步的输出
  • 输出：三角形面片数据
• 光栅化 Rasterization
  • 输入：上一步的输出
  • 输出：一个个的像素数据(片元数据)
• 片元处理 Fragment Processing
  • 输入：上一步的输出
  • 输出：每个像素的颜色数据
• 后期处理 Framebuffer Processing
  • 输入：上一步的输出
  • 输出：最终显示出的图像数据

Sharder 编程

现代 GPU 允许用户编写自己的着色器程序来控制渲染管线的某些阶段。

如 OpenGL 允许使用 GLSL 定义 Vertex Processing 和 Fragment Processing 的着色器程序。

如下代码片段定义了一个简单的片元着色器，对于每个像素都会执行以下程序片段：

// uniform 是全局变量，是CPU传递给 GPU 的数据，在绘制过程中保持不变
uniform sampler2D myTexture; // 纹理采样器
uniform vec3 lightDir; // 光源方向

// varying 是顶点着色器传递过来的变量
verying vec2 uv; // 顶点着色器传递过来的纹理坐标
varying vec3 norm; // 顶点着色器传递过来的法向量

void diffuseShader() {
    vec3 kd = texture2d(myTexture, uv).rgb; // 从纹理中采样颜色
    kd *= clamp(dot(-lightDir, norm), 0.0, 1.0); // 计算漫反射光照强度
    gl_FragColor = vec4(kd, 1.0); // 最终颜色输出
}

Shardertoy 是一个在线的着色器编程平台，允许用户编写自己的着色器程序并实时预览效果。里面会有很多好玩的着色器示例。

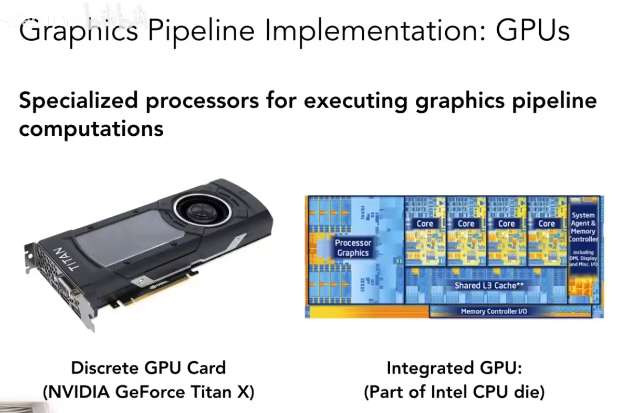
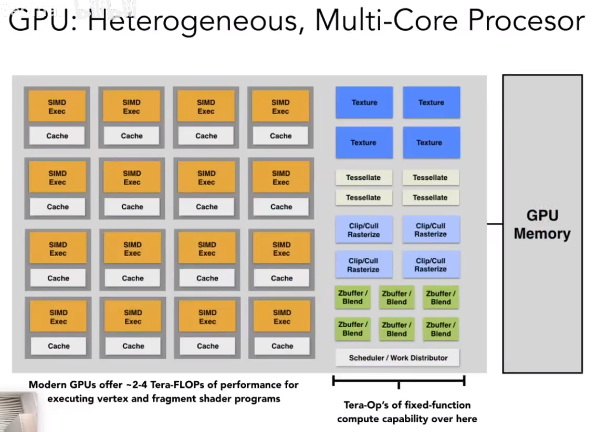
图形管线的硬件实现 GPU

图形管线的硬件实现即为 GPU，GPU 是专门为图形渲染而设计的处理器，具有高度并行的计算能力。

纹理 Texture

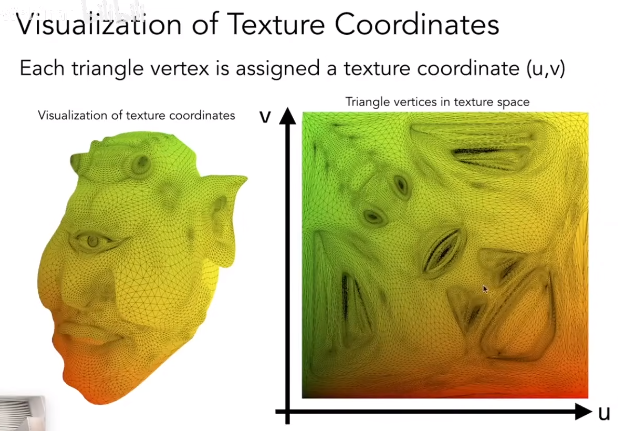
纹理映射 Texture Mapping

每个三维物体的表面都可以映射到一个二维的纹理图像上，反之亦然。这个过程称为纹理映射。

为了方便处理，通常把 u,v 坐标归一化到$[0,1]$区间内。

纹理映射也可以反复重复多次，不一定只能使用一次。

基于重心坐标的三角形插值 Barycentric Coordinates

为什么需要插值？

• 当计算出三角形的顶点属性后，需要计算三角形内部任意一点的属性
• 并且且需要保证插值的属性在三角形内部是足够平滑过渡的
• 我们希望计算的属性有: 纹理坐标，颜色，法向量… 等

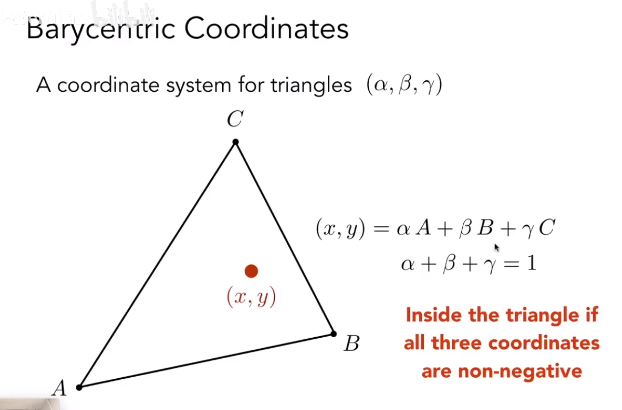
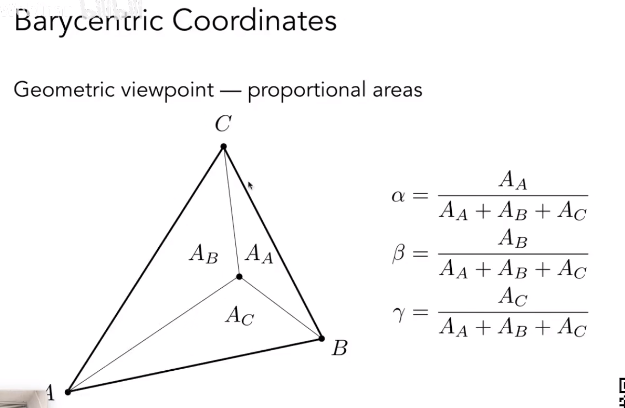
三角形平面内的任意一点 P 都可以表示为顶点 A, B, C 的线性组合：

$P = \alpha A + \beta B + \gamma C$

其中 $\alpha + \beta + \gamma = 1$，且 $\alpha, \beta, \gamma \geq 0$。

$\alpha, \beta, \gamma$ 就是点 P 的重心坐标。

三角形内任意一点 P 的重心坐标可以通过面积比计算得到：

$\alpha = \frac{area(PBC)}{area(ABC)}, \beta = \frac{area(PCA)}{area(ABC)}, \gamma = \frac{area(PAB)}{area(ABC)}$

若点 P 是三角形的重心，则 $\alpha = \beta = \gamma = \frac{1}{3}$。重心和三个顶点组成的三个三角形面积相等。

也可以基于面积比结合叉乘，直接得到最终的重心坐标公式：

$\alpha = \frac{-(x-x_B)(y_C-y_B) + (y-y_B)(x_C-x_B)}{-(x_A-x_B)(y_C-y_B) + (y_A-y_B)(x_C-x_B)}$

$\beta = \frac{-(x-x_C)(y_A-y_C) + (y-y_C)(x_A-x_C)}{-(x_B-x_C)(y_A-y_C) + (y_B-y_C)(x_A-x_C)} \\$

$\gamma = 1 - \alpha - \beta$

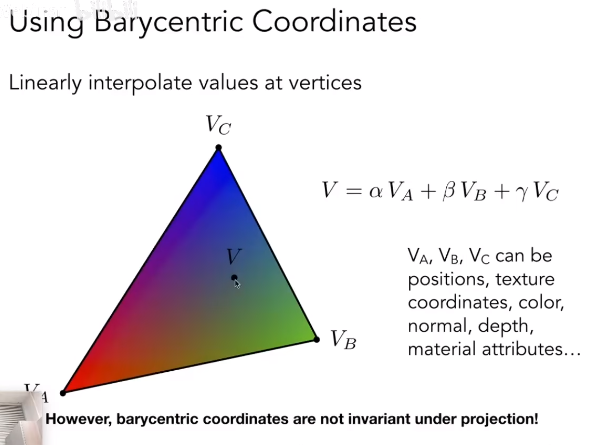
计算出某一点的重心坐标后，可以通过重心坐标对各个顶点属性进行插值计算。

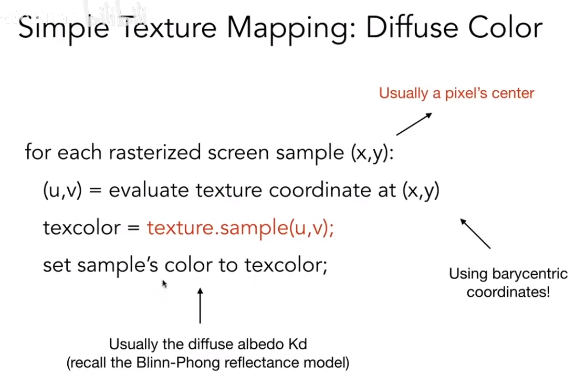
纹理映射——漫反射颜色

对于屏幕上的每一个采样点（像素中心）的(x,y)坐标，都可以映射到一个纹理坐标(u, v)中，求出该纹理坐标对应的颜色 texcolor = texture.sample(u,v)，然后将该颜色作为漫反射颜色 kd = texcolor。

纹理放大 Texture Magnification

一个像素点(pixel)对应到纹理的像素点是 texel，当纹理太小时，可能会出现多个像素点对应到同一个纹理像素点的情况，这时就需要对纹理进行插值计算，得到该像素点的颜色。

Nearest 最近点采样

第一张图使用了一种 Nearest 的采样方式，直接取离纹理坐标最近的一个纹理像素点的颜色作为该像素点的颜色。效果可能会比较粗糙，可以看到明显的锯齿。

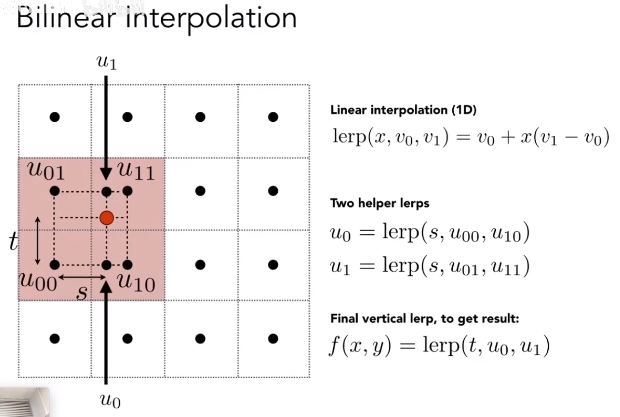
Bilinear 双线性插值

第二张图使用了 Bilinear 的采样方式，取离纹理坐标最近的四个纹理像素点的颜色进行双线性插值计算，得到该像素点的颜色。效果会比 Nearest 好很多。

定义一维线性插值函数：

$lerp(x,v_0,v_1)=v_0 + (v_1 - v_0) \cdot x$

$x$ 的范围是 $[0,1]$，当 $x=0$ 时，返回 $v_0$；当 $x=1$ 时，返回 $v_1$。

对如图所示的四个点$u_{01}, u_{11}, u_{10}, u_{00}$进行双线性插值的步骤如下：

先在水平方向分别对 $u_{01}, u_{11}$ 和 $u_{00}, u_{10}$ 进行线性插值，得到两个中间点：

$u_{0} = lerp(x, u_{00}, u_{10}) \\ u_{1} = lerp(x, u_{01}, u_{11})$

最终这两个点位于同一个竖直方向上，再对这两个点进行线性插值，得到最终的插值结果：

$f(x,y) = lerp(y, u_{0}, u_{1})$

Bicubic 双三次插值

第三张图使用了 Bicubic 的采样方式，取离纹理坐标最近的 16 个纹理像素点的颜色进行双三次插值计算，得到该像素点的颜色。效果会比 Bilinear 好很多。

纹理缩小 Texture Minification

当纹理太大时，可能会出现一个像素覆盖了很多个纹理像素的情况，这时就需要对纹理进行缩小处理，得到该像素点的颜色。

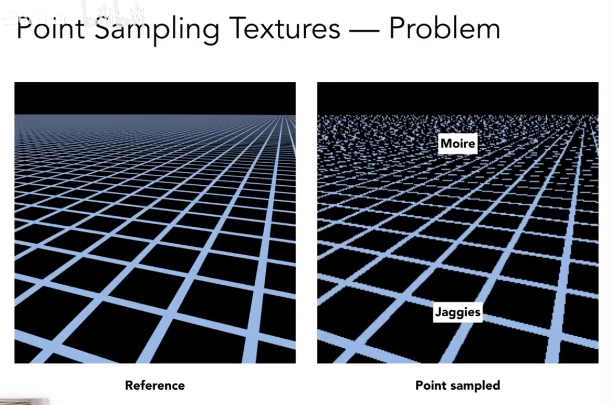
例如，图中的纹理图像太高清，当直接对纹理图像进行采样时，远处密集的像素会产生摩尔纹现象，近处的像素会产生锯齿现象。

本质上是因为采样率不够导致了丢失了高频信息。

一种解决方案是对要求的像素点对应的纹理点周围的像素点进行平均，得到一个新的纹理像素点，这样可以减少高频信息的丢失。

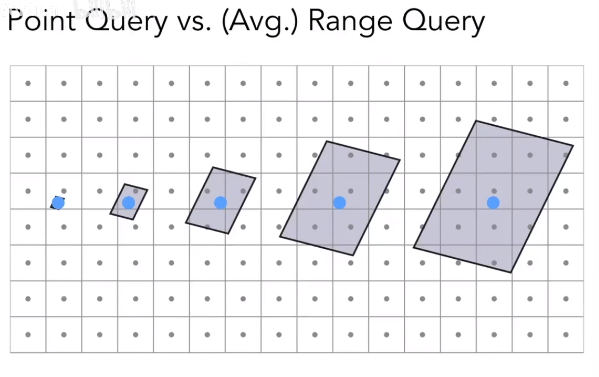
点查询和范围查询

为了优化查询性能，在数据结构，计算几何等领域有两种查询模型，分别称为点查询和范围查询。

点查询是指查询一个具体的点，返回该点对应的数据。

范围查询是指查询一个区域内的所有点，返回该区域内所有点经过某些处理后的数据。

这里我们只需要用到范围查询来求范围点的平均值。

Mipmap

允许快速，近似地，对正方形的纹理进行范围查询。

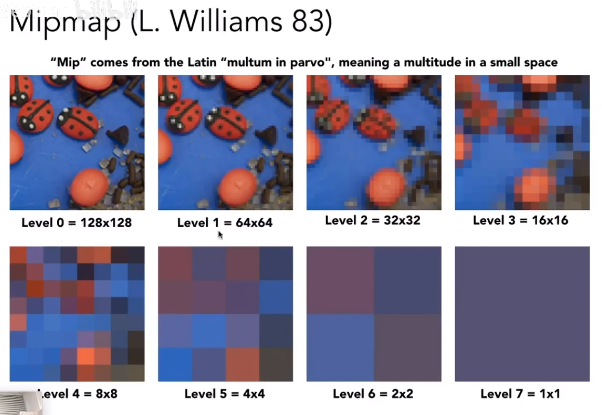
Mipmap 是一种多分辨率纹理存储方式，通常用于纹理缩小时的采样。

它是一种分层次化的纹理存储方式，包含了多个不同分辨率的纹理图像。

假设原始纹理图像的分辨率为 $2^n \times 2^n$，则 Mipmap 会包含 $n+1$ 层纹理图像，每一层的分辨率都是上一层的一半。

通过这样冗余存储不同分辨率的纹理图像，可以在缩小纹理时，快速地选择合适的纹理图像进行采样。

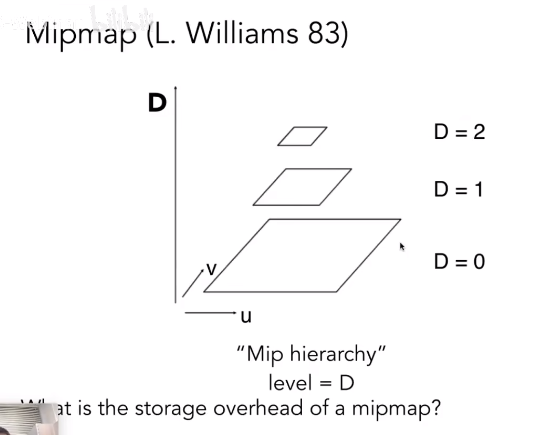
冗余率计算：

$\text{冗余率} = \frac{\text{总纹理像素数}}{\text{原始纹理像素数}} = \frac{1 + \frac{1}{4} + \frac{1}{16} + \ldots + \frac{1}{4^n}}{1} = \frac{1}{1 - \frac{1}{4}} = \frac{4}{3}$

最终计算得到 mipmap 之后相比于原始纹理图像，冗余率为 $4/3$，即多存储了 $\frac{1}{3}$ 的纹理像素数据。

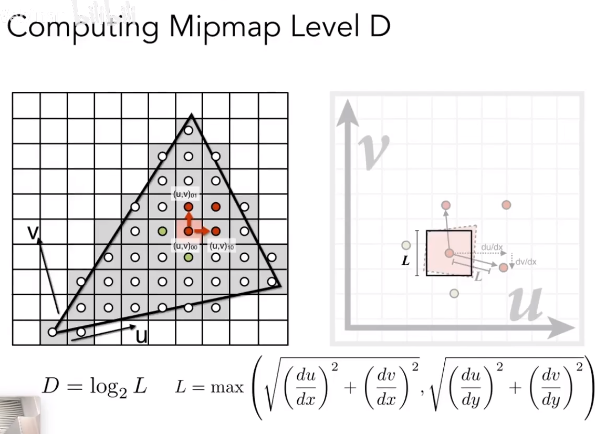
查询过程：

将原始像素点的邻近像素映射到 u,v 坐标中，求 uv 坐标系下的两像素点之间的距离，水平竖直方向上取一个最大的值作为$L$，再计算$D=log_2(L)$，得到 mipmap 的层数 $i$，即 $i = \lfloor D \rfloor$。此时原始像素点在第 $i$ 层的 mipmap 中只对应了一个像素点了，不再存在多个像素点，实际上也就间接完成了平均值的范围查询。

现代 GPU 中的纹理

在现代 GPU 中，纹理本质上就是一块内存区域的数据，并且可以快速高效地做范围查询，做采样等。

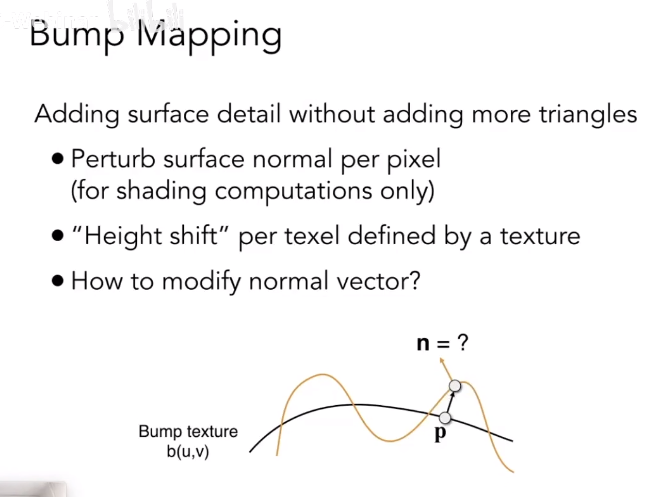
凹凸贴图 Dump Texture

一个光滑的物体表面，可以通过一个凹凸贴图描述物体表面存在细微的凹凸扰动，从而改变物体表面的法向量，进而影响光照着色计算。

一维凹凸贴图

在 flatland 的一维空间中，凹凸贴图可以看作是一个一维的高度图，表示物体表面的高度变化。法向量计算如下：

• 定义 p 点原始的法向量为$n(p)=(0,1)$
• 定义 p 点的凹凸贴图高度为 $h(p)$
• 对 p 点求梯度，假设水平方向前进单位 1，则竖直方向上变化 $dp = c * (h(p+1) - h(p))$
• 切线向量为 $t(p)=(1,dp)$
• 法向量为 $n(p) = (-dp, 1)$

二维凹凸贴图

在三维空间中，凹凸贴图可以看作是一个二维的高度图，表示物体表面的高度变化。法向量计算如下：

• 定义 p 点原始的法向量为$n(p)=(0,0,1)$
• 定义 p(u,v) 点的凹凸贴图高度为 $h(u,v)$
• 对 p 点求梯度，假设平面的两个正交的方向上分别前进单位 1，则
  • u 方向前进单位 1，v 方向不变 $dp/du = c1 * (h(u+1,v) - h(u,v))$
  • u 方向不变，v 方向前进单位 1 $dp/dv = c2 * (h(u,v+1) - h(u,v))$
• 法向量为：$n(p) = (-dp/du, -dp/dv, 1)$

位移贴图 Displacement Mapping

位移贴图实际改变了物体表面的几何形状，而不是仅仅改变物体表面的法向量。

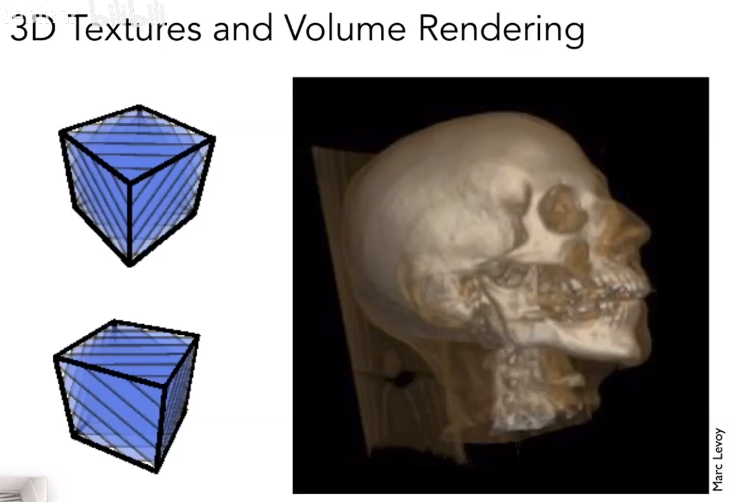
三维纹理

纹理还可以是三维的，表示空间中任意一个点的纹理数据。

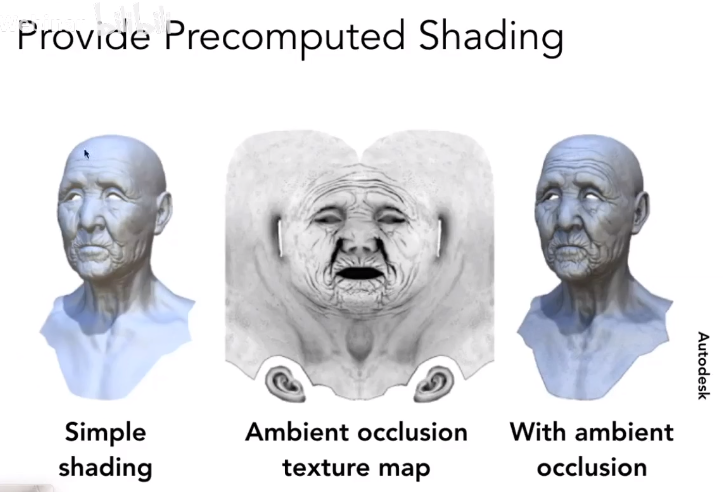
纹理还可以预计算一些数据

体积纹理可以用来表示三维纹理数据，如医学成像中的 CT 扫描数据。