数学建模-线性规划-投资规划问题

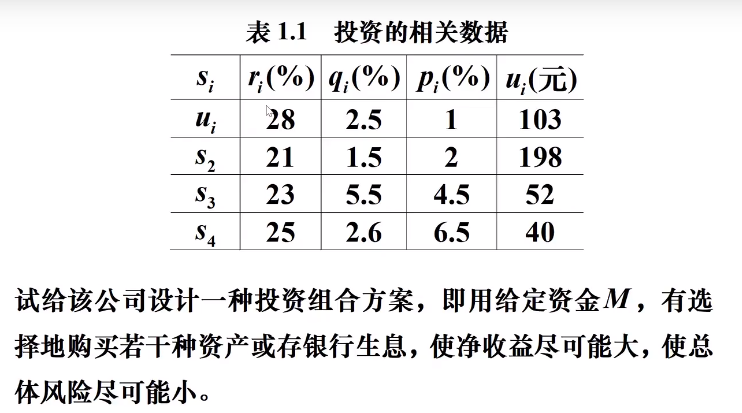
题目

数学建模

符号规定

$s_i表示第i种投资项目，i = 0,1,2,..,n$

$r_i表示s_i的平均收益率$

$p_i表示s_i的交易费率$

$q_i表示s_i的风险损失率$

$u_i表示交易定额，即s_i产品最少也要花u_i元$

$x_i表示投资项目s_i的资金$

$a表示投资风险度，越小越好$

$Q表示总体收益，越大越好$

模型假设

投资数额M相当大
投资越分散，总风险越小
总体风险用投资项目 $s_i$ 中最大的风险度量
$n+1$ 种资产 $s_i$ 相互独立
在投资时期内， $r_i,p_i,q_i$ 均为定值，不受其他因素影响， $p_0=0,q_0=0$
净收益和总体风险只受 $r_i,p_i,q_i$ 的影响，不受其他因素的干扰

模型建立

总体风险用所投资的 $s_i$ 中最大的一个风险来度量，即

$max\{ q_i x_i | i=1,2,3,...,n \}$

购买 $s_i$ 所付的交易费是一个分段函数，即

$交易费= \left\{ \begin{array}{l} p_i x_i, \space x_i > u_i \\ p_i u_i, \space x_i \leq u_i \\ \end{array} \right.$

故购买 $s_i$ 的 $净收益=平均收益-交易费=r_i x_i - 交易费$ ，由于 $u_i$ 相对于总投资 $M$ 相当小，故净收益可简化为 $(r_i-p_i)x_i$

规划目标是使净收益增大，总体风险尽量小，故本模型为多目标规划模型。

得到初步的多目标规划模型如下

$\left\{ \begin{array}{l} max \space \sum_{i=0}^{n} {(r_i-p_i)x_i} \\ min \space max\{ q_i x_i \} \end{array} \right. \\ s.t. = \left\{ \begin{array}{l} \sum_{i=0}^{n} {(1+p_i)x_i} = M \\ x_i \geq 0, \space i=0,1,...,n \end{array} \right.$

模型一

该模型的目标函数(2)表示总体风险尽可能的小，那么多小是小呢？此时可以设定一个界限，当小于等于某个数值时表示可接受的风险水平。这种条件下，可导出模型一如下，

固定风险水平，引入一个参数 $\alpha < 1$ ，设实际投资中，投资者能够承担的最大风险为 $\alpha M$ ，则有 $max\{q_i x_i\} \leq \alpha M$ ，即对于任意的 $i$ 均有 $q_i x_i \leq \alpha M$ ，则原模型可简化为

$max \space \sum_{i=0}^{n} {(r_i-p_i)x_i} \\ s.t. = \left\{ \begin{array}{l} q_i x_i \leq \alpha M \\ \sum_{i=0}^{n} {(1+p_i)x_i} = M \\ x_i \geq 0, \space i=0,1,...,n \end{array} \right.$

模型二

该模型目标函数(1)表示要使得净收益最大，设定界限，只要总的净收益不低于k即可接受净收益。这种条件下，可导出模型二如下，

$min \space max\{ q_i x_i \} \\ s.t. = \left\{ \begin{array}{l} \sum_{i=0}^{n} {(r_i-p_i)x_i} \geq k \\ \sum_{i=0}^{n} {(1+p_i)x_i} = M \\ x_i \geq 0, \space i=0,1,...,n \end{array} \right.$

模型三

权衡投资风险与预期收益时，对风险与收益给予权重分别为 $s,\space(1-s),s \in (0,1]$ ，这反映了投资者重视风险还是重视收益，s为投资偏好系数。则目标可转化为使得风险-收益最小，或收益-风险最大，可导出模型三如下，

$min \space \{s(max\{q_i x_i\})-(1-s)\sum_{i=0}^{n} {(r_i-p_i)x_i}\} \\ s.t. = \left\{ \begin{array}{l} \sum_{i=0}^{n} {(1+p_i)x_i} = M \\ x_i \geq 0, \space i=0,1,...,n \end{array} \right.$

模型求解

由于建模时为了简化模型，将 $u_i$ 不考虑了，故导出的数学模型与 $u_i$ 无关，那么M便不受约束了，为了方便期间这里假设M=1

模型一求解

模型一如下，

$max \space \sum_{i=0}^{n} {(r_i-p_i)x_i} \\ s.t. = \left\{ \begin{array}{l} q_i x_i \leq \alpha M \\ \sum_{i=0}^{n} {(1+p_i)x_i} = M \\ x_i \geq 0, \space i=0,1,...,n \end{array} \right.$

根据题目可得，

r = (0.05, 0.28, 0.21 ,0.23 ,0.25)
p = (0, 0.01, 0.02, 0.045, 0.065)
q = (0, 0.025, 0.015, 0.055, 0.026)
M = 1
a从0到0.05步长0.001遍历搜索答案

首先编写如下函数用于根据给定参数，求解规划目标

function [x,Q] = fun(r,p,q,M,a)
% 目标函数系数列向量
f = -(r-p)';

% 不等式约束系数矩阵
A = diag(q);
% 不等式约束常数列向量
b = a*ones(5,1);

% 等式约束系数矩阵
Aeq = 1+p;
% 等式约束常数列向量
beq = [M];
 
% 目标解约束下界
lb = zeros(5,1);
% ub = ((a * M)./q)';
ub = [];
[x,fval] = linprog(f,A,b,Aeq,beq,lb,ub);

x = x;
Q = -fval;
end

编写以下代码，用于给定参数与遍历a来搜索答案并绘制a-Q散点图


clc,clear;
hold on;
% 输入参数
r = [0.05, 0.28, 0.21 ,0.23 ,0.25];
p = [0, 0.01, 0.02, 0.045, 0.065];
q = [0, 0.025, 0.015, 0.055, 0.026];
M = 1;

for a = 0:0.001:0.05
    [x,Q] = fun(r,p,q,M,a);
    plot(a,Q,'.k');
end
xlabel('a'),ylabel('Q');