S-DES加密过程 | 字数总计: 2.4k | 阅读时长: 12分钟 | 阅读量: |
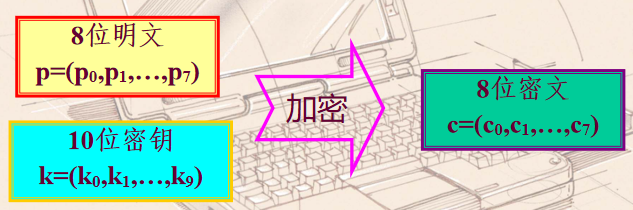
已知10位的种子密钥k = ( k 0 , k 1 , . . . , k 9 ) k=(k_0,k_1,...,k_9) k = ( k 0 , k 1 , . . . , k 9 )
执行P 10 P10 P 1 0 m 1 = P 10 ( k ) m_1=P10(k) m 1 = P 1 0 ( k )
5位一组分割成两组,每组内循环左移s位记作变换S L s SL_s S L s m 1 m_1 m 1 m 2 = S L 1 ( m 1 ) m_2=SL_1(m_1) m 2 = S L 1 ( m 1 )
执行10位变8位的P8置换变换得到k 1 = P 8 ( m 2 ) k_1=P8(m_2) k 1 = P 8 ( m 2 )
对m 2 m_2 m 2 m 3 = S L 2 ( m 2 ) m_3=SL_2(m_2) m 3 = S L 2 ( m 2 )
执行10位变8位的P8置换变换得到k 2 = P 8 ( m 3 ) k_2=P8(m_3) k 2 = P 8 ( m 3 )
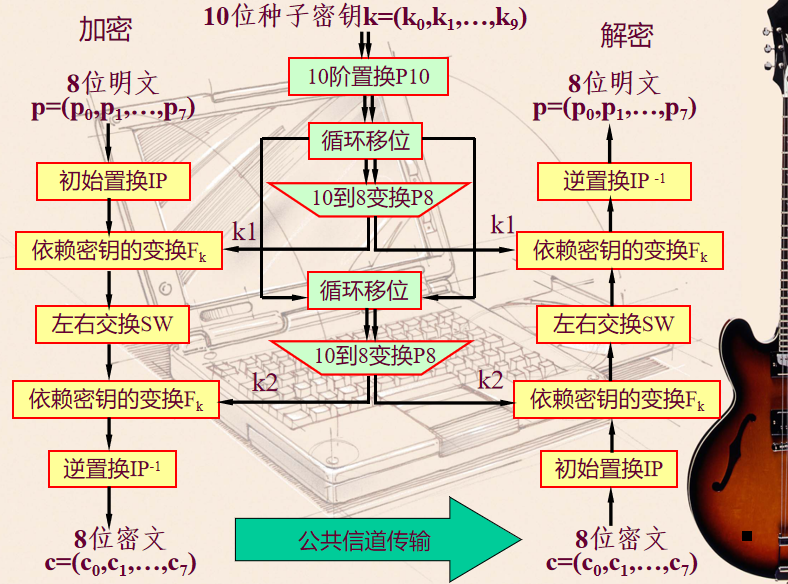
先来看加密算法,已知明文p p p
对p p p I P IP I P I P ( p ) IP(p) I P ( p )
对I P ( p ) IP(p) I P ( p ) k 1 k_1 k 1 F k 1 F_{k_1} F k 1 F k 1 ( I P ( p ) ) F_{k_1}(IP(p)) F k 1 ( I P ( p ) )
对F k 1 ( I P ( p ) ) F_{k_1}(IP(p)) F k 1 ( I P ( p ) ) S W SW S W S W ( F k 1 ( I P ( p ) ) ) SW(F_{k_1}(IP(p))) S W ( F k 1 ( I P ( p ) ) )
对S W ( F k 1 ( I P ( p ) ) ) SW(F_{k_1}(IP(p))) S W ( F k 1 ( I P ( p ) ) ) k 2 k_2 k 2 F k 2 F_{k_2} F k 2 F k 2 ( S W ( F k 1 ( I P ( p ) ) ) ) F_{k_2}(SW(F_{k_1}(IP(p)))) F k 2 ( S W ( F k 1 ( I P ( p ) ) ) )
对F k 2 ( S W ( F k 1 ( I P ( p ) ) ) ) F_{k_2}(SW(F_{k_1}(IP(p)))) F k 2 ( S W ( F k 1 ( I P ( p ) ) ) ) I P IP I P I P − 1 {IP}^{-1} I P − 1 c = I P − 1 ( F k 2 ( S W ( F k 1 ( I P ( p ) ) ) ) ) c={IP}^{-1}(F_{k_2}(SW(F_{k_1}(IP(p))))) c = I P − 1 ( F k 2 ( S W ( F k 1 ( I P ( p ) ) ) ) )
再看解密算法,解密算法实际上仅仅只是将上述加密流程中的k 1 , k 2 k_1,k_2 k 1 , k 2
加密公式:c = I P − 1 ( F k 2 ( S W ( F k 1 ( I P ( p ) ) ) ) ) c={IP}^{-1}(F_{k_2}(SW(F_{k_1}(IP(p))))) c = I P − 1 ( F k 2 ( S W ( F k 1 ( I P ( p ) ) ) ) )
解密公式:p = I P − 1 ( F k 1 ( S W ( F k 2 ( I P ( c ) ) ) ) ) p={IP}^{-1}(F_{k_1}(SW(F_{k_2}(IP(c))))) p = I P − 1 ( F k 1 ( S W ( F k 2 ( I P ( c ) ) ) ) )
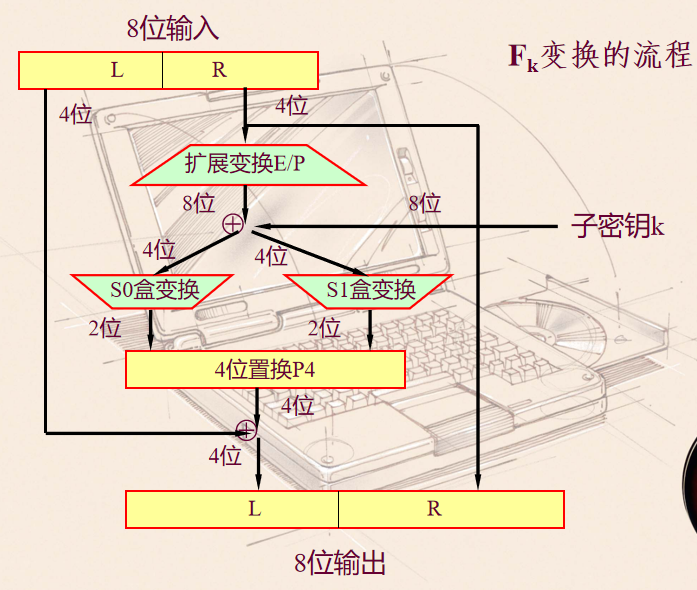
F k F_k F k k k k
取右半四位二进制R R R E / P E/P E / P E / P ( R ) E/P(R) E / P ( R )
与8位子密钥k k k E / P ( R ) ⊕ k E/P(R) \oplus k E / P ( R ) ⊕ k
取E / P ( R ) ⊕ k E/P(R) \oplus k E / P ( R ) ⊕ k
L 1 , R 1 L1, R1 L 1 , R 1 S 0 , S 1 S0,S1 S 0 , S 1 L 2 , R 2 L2,R2 L 2 , R 2
L 2 , R 2 L2, R2 L 2 , R 2 P 4 P4 P 4 P 4 ( L 2 , R 2 ) P4(L2, R2) P 4 ( L 2 , R 2 )
记输出结果为L 3 , R 3 L3, R3 L 3 , R 3 R 3 = R , L 3 = L ⊕ P 4 ( L 2 , R 2 ) R3=R, L3=L \oplus P4(L2, R2) R 3 = R , L 3 = L ⊕ P 4 ( L 2 , R 2 )
使用c++实现S-DES加密算法
代码中涉及大量二进制位操作,使用c++标准库的bitset作为存储结构
注意bitset的打印输出低位在右侧,而书面解释时,一般低位在左侧。
代码较为简单,仅仅只是查表,填充,即仅二进制位置发生变换,不改变二进制中的位(原来分别有多少0,1现在还是有多少)
1 2 3 4 5 6 bitset<10> P10 (bitset<10 > in) { const int table[] = {3 , 5 , 2 , 7 , 4 , 10 , 1 , 9 , 8 , 6 }; bitset<10> out; for (int i = 0 ; i < 10 ; i++) out[i] = in[table[i] - 1 ]; return out; }
同P10变换的原理
1 2 3 4 5 6 bitset<8> P8 (bitset<10 > in) { const int table[] = {6 , 3 , 7 , 4 , 8 , 5 , 10 , 9 }; bitset<8> out; for (int i = 0 ; i < 8 ; i++) out[i] = in[table[i] - 1 ]; return out; }
1 2 3 4 5 6 template <size_t N>bitset<N> rol (bitset<N> src, int size) { size = (size + N) % N; return src << size | src >> (N - size); }
5位一组分割成两组,每组内循环左移s位记作变换S L s SL_s S L s
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 bitset<10> SL (bitset<10 > in, int s) { bitset<5> left, right; for (int i=0 ;i<5 ;i++) left[i] = in[i]; for (int i=0 ;i<5 ;i++) right[i] = in[i+5 ]; left = rol <5 >(left, -s); right = rol <5 >(right, -s); bitset<10> out; for (int i=0 ;i<5 ;i++) out[i] = left[i]; for (int i=0 ;i<5 ;i++) out[i+5 ] = right[i]; return out; }
1 2 3 4 5 6 7 8 9 10 void subkey (bitset<10 > in, bitset<8 >& out_k1, bitset<8 >& out_k2) bitset<10> m1 = P10 (in); bitset<10> m2 = SL (m1,1 ); out_k1 = P8 (m2); bitset<10> m3 = SL (m2,2 ); out_k2 = P8 (m3); }
1 2 3 4 5 6 bitset<8> IP (bitset<8 > in) { const int table[] = {2 , 6 , 3 , 1 , 4 , 8 , 5 , 7 }; bitset<8> out; for (int i = 0 ; i < 8 ; i++) out[i] = in[table[i] - 1 ]; return out; }
1 2 3 4 5 6 bitset<8> IP_rev (bitset<8 > in) { const int table[] = {4 , 1 , 3 , 5 , 7 , 2 , 8 , 6 }; bitset<8> out; for (int i = 0 ; i < 8 ; i++) out[i] = in[table[i] - 1 ]; return out; }
输入4位输出8位的E/P扩展置换变换
1 2 3 4 5 6 7 bitset<8> E_P (bitset<4 > in) { const int table[] = {4 , 1 , 2 , 3 , 2 , 3 , 4 , 1 }; bitset<8> out; for (int i = 0 ; i < 8 ; i++) out[i] = in[table[i] - 1 ]; return out; }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 bitset<2> S0 (bitset<4 > in) { const int table[4 ][4 ] = { {1 , 0 , 3 , 2 }, {3 , 2 , 1 , 0 }, {0 , 2 , 1 , 3 }, {3 , 1 , 3 , 2 }}; int i = in[0 ] << 1 | in[3 ]; int j = in[1 ] << 1 | in[2 ]; return table[i][j]; } bitset<2> S1 (bitset<4 > in) { const int table[4 ][4 ] = { {0 , 1 , 2 , 3 }, {2 , 0 , 1 , 3 }, {3 , 0 , 1 , 0 }, {2 , 1 , 0 , 1 }}; int i = in[0 ] << 1 | in[3 ]; int j = in[1 ] << 1 | in[2 ]; return table[i][j]; }
1 2 3 4 5 6 bitset<4> P4 (bitset<4 > in) { const int table[] = {2 , 4 , 3 , 1 }; bitset<4> out; for (int i = 0 ; i < 8 ; i++) out[i] = in[table[i] - 1 ]; return out; }
1 2 3 4 5 6 7 8 9 10 11 12 bitset<8> F (bitset<8 > in, bitset<8 > k) { bitset<4> in_L, in_R; for (int i = 0 ; i < 4 ; i++) in_L[i] = in[i]; for (int i = 0 ; i < 4 ; i++) in_R[i] = in[4 + i]; bitset<4> out_L = in_L ^ P4 (S (E_P (in_R) ^ k)); bitset<4> out_R = in_R; bitset<8> out; for (int i = 0 ; i < 4 ; i++) out[i] = out_L[i]; for (int i = 0 ; i < 4 ; i++) out[i+4 ] = out_R[i]; return out; }
1 2 3 4 5 6 7 8 9 10 11 bitset<8> SW (bitset<8 > in) { bitset<4> in_L, in_R; for (int i = 0 ; i < 4 ; i++) in_L[i] = in[i]; for (int i = 0 ; i < 4 ; i++) in_R[i] = in[4 + i]; bitset<4> out_L = in_R; bitset<4> out_R = in_L; bitset<8> out; for (int i = 0 ; i < 4 ; i++) out[i] = out_L[i]; for (int i = 0 ; i < 4 ; i++) out[i+4 ] = out_R[i]; return out; }
定义通用加解密流程如下
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 bitset<8> crypt (bitset<8 > p, bitset<8 > k1, bitset<8 > k2) { bitset<8> IP_out = IP (p); bitset<8> Fk1_out = F (IP_out, k1); bitset<8> SW_out = SW (Fk1_out); bitset<8> Fk2_out = F (SW_out, k2); bitset<8> IP_rev_out = IP_rev (Fk2_out); return IP_rev_out; }
加密解密的函数模块入口可实现如下,
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 bitset<8> encrypt (bitset<8 > p, bitset<10 > k) { bitset<8> k1, k2; subkey (k, k1, k2); return crypt (p, k1, k2); } bitset<8> decrypt (bitset<8 > p, bitset<10 > k) { bitset<8> k1, k2; subkey (k, k1, k2); return crypt (p, k2, k1); }
实现反向输出bitset的函数
1 2 3 4 5 6 template <int T>string reverse (bitset<T> src) { stringstream ss; for (int i = 0 ; i < src.size (); i++) ss << src[i]; return ss.str (); }
主函数
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 int main () int _k[] = {1 , 0 , 1 , 0 , 0 , 0 , 0 , 0 , 1 , 0 }; bitset<10> k; for (int i = 0 ; i < 10 ; i++) k[i] = _k[i]; int _p[] = {0 , 1 , 0 , 0 , 0 , 0 , 0 , 1 }; bitset<8> p; for (int i = 0 ; i < 8 ; i++) p[i] = _p[i]; auto c = encrypt (p, k); cout << "密文=" << reverse <8 >(c) << endl; auto mp = decrypt (c, k); cout << "明文=" << reverse <8 >(mp) << endl; return 0 ; }
输出结果
2、已知种子密钥k=0111111101,
1
2
3
4
5
6
7
8
9
10
3
5
2
7
4
10
1
9
8
6
1
2
3
4
5
6
7
8
6
3
7
4
8
5
10
9
(1)试采用S-DES算法计算子密钥K1,K2。
m1=P10(k)=11111,10011
m1分组后各自循环左移1位得到m2=11111,00111
m2分组后各自循环左移2位得到m3=11111,11100
K1=P8(m2)=01011111
K2=P8(m3)=11111100
(2)若明文p=10011101,试用S-DES算法给出加密过程,要有中间步骤。
p1=IP§ = 01011110
输入如下:
p1=01011110
k1=01011111
L1=0101, R1=1110
p2=E/P(R1)=0111101
p3=p2^k1=00100010
L2=0010, R2=0010
S0(L2)=S0_01=00
S1(R2)=S1_01=01
p4=P4(S0||S1=0001)=0100
L3 = p4^L1=0001
R3=1110
p5=Fk1(p1)=00011110
p6=11100001
输入如下,
p6=11100001
k2=11111100
与Fk1同理可得
p7=Fk2(p6)=11100001
c=I P − 1 ( p 7 ) IP^{-1}(p7) I P − 1 ( p 7 )
故密文为c=01100110