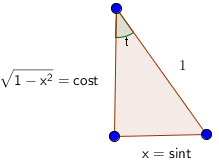以下公式仅用于辅助记忆,不可用于证明题,求积分公式本身的题目。
公式1
∫a2−x2dx=2xa2−x2+2a2arcsinax+C

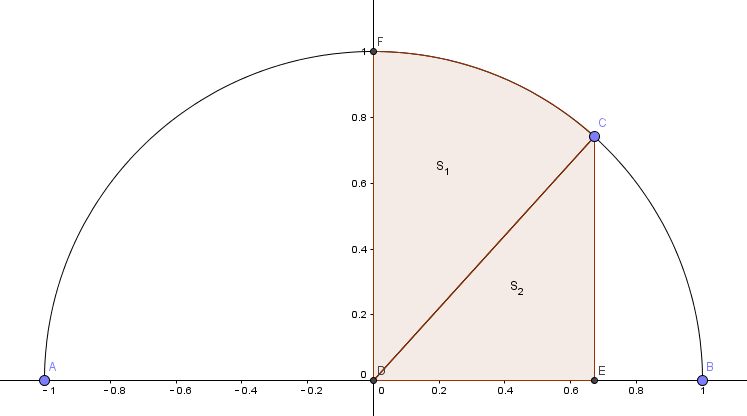
如图,函数y=a2−x2 为上图的半圆,则原函数可表示为S=∫axa2−x2dx,不妨设a=0,x=xC,则S为如图阴影部分的面积。
阴影部分可拆分成两部分S1,S2,
三角形部分的S2可表示如下
S2=21xCyC=2xa2−x2
扇形部分的S1可表示如下,设扇形的角度α
α=∠CDF=∠DCE=arcsinRxC=arcsinax
扇形的面积S1
S1=21αR2=2a2arcsinax
故得出S
S=S1+S2=2xa2−x2+2a2arcsinax
原不定积分添加常数C,即得到积分公式
∫a2−x2dx=2xa2−x2+2a2arcsinax+C
公式2
∫x2−a2dx=2xx2−a2−2a2ln∣x+x2−a2∣+C
PS: 这里暂时只说明当x>0时的情况
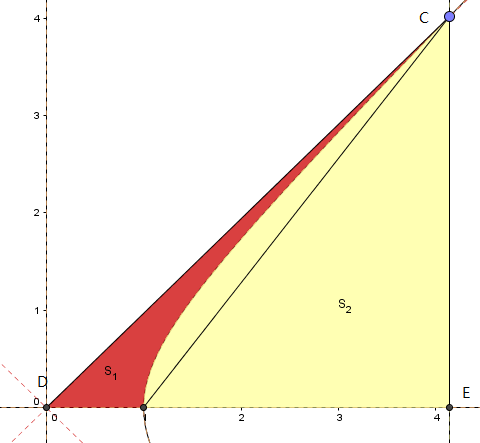
y=x2−a2即a2x2−a2y2=1,y≥0,可画出如下图形

如图,原函数可表示为S2=∫bxx2−a2dx,不妨设b=a,x=xC
S=SΔCDE==S1+S2
S=21DE×CE=2xx2−a2
S1可由双曲函数的定义出发得出,
双曲余弦函数_百度百科 (baidu.com)
对于双曲线x2−y2=a2而言,
设coshα=ax则有
S1=21a2α=21a2arccoshax
其中反双曲余弦可表示如下
arccoshx=ln(x+x2−1)
arccoshax=ln(x+x2−a2)−lna
S1=2a2ln(x+x2−a2)+C1
得到
S2=S−S1=2xx2−a2−2a2ln(x+x2−a2)+C
当x<0时同理,最终得到以下积分公式
∫x2−a2dx=2xx2−a2−2a2ln∣x+x2−a2∣+C
公式3
∫x2+a2dx=2xx2+a2+2a2ln(x+x2+a2)+C
实际上是公式2的双曲线焦点在y轴时的场景,记忆方式同公式2
公式4
∫sec3xdx=21secx tanx+21ln∣secx+tanx∣
该公式还可使用分部积分完成计算
PS: 这里只说明secx>0时的情况
∫sec3xdx=∫secx dtanx

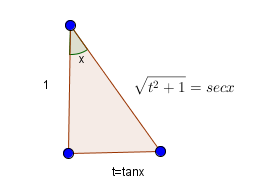
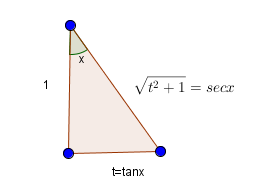
令t=tanx,则secx=t2+1
∫secx dtanx=∫t2+1 dt=2tt2+1+21ln(t+t2+1)+C
∫sec3xdx=21secx tanx+21ln(secx+tanx)+C
公式5
∫csc3xdx=−21cscx cotx+21ln∣cscx−cotx∣+C
同公式4
公式6
∫secx dx=ln∣secx+tanx∣+C
PS: 这里只考虑secx>0的情况

dt=sec2x dx
∫secx dx=∫t2+11dt=ln(t+t2+1)+C=ln(tanx+secx)+C
考虑secx<0时,则有
∫secx dx=ln∣secx+tanx∣+C
公式7
∫x2+a21dx=ln(x+x2+a2)+C=arcsinhax+C

如图换元并应用公式6得到
∫t2+11dt=∫secx dx=ln∣secx+tanx∣+C=ln(t+t2+1)+C=arcsinhx+C∫x2+a21dx=∫(ax)2+11dax=ln(ax+(ax)2+1)+C1=ln(x+x2+a2)+C2=arcsinhax+C
公式8
∫x2−a21dx=2a1ln∣x+ax−a∣+C

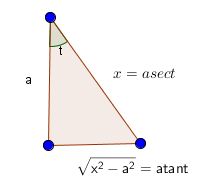
∫x2−a21dx=∫(atant)21a sect tant dt=a1∫csct dt=a1ln∣csct−cott∣+C=2a1ln∣sin2t(1−cost)2∣+C=2a1ln∣1−cos2t(1−cost)2∣+C=2a1ln∣(1−cost)(1+cost)(1−cost)2∣+C=2a1ln∣1+cost1−cost∣+C=2a1ln∣1+xa1−xa∣+C=2a1ln∣x+ax−a∣+C
公式9
∫x2+a21dx=a1arctanax+C

换元得
∫t2+11dt=∫sec2x1sec2x dx=x+C=arctant+C
∫x2+a21dx=a1∫(ax)2+11dax=a1arctanax+C
公式10
∫a2−x21dx=arcsinax+C

∫1−x21dx=∫cost1cost dt=t+C=arcsinx+C
∫a2−x21dx=∫1−(ax)21dax=arcsinax+C
若将t设为另一个互补的角,则可得到另一个有意思的结果
∫1−x21dx=−∫sint1sint dt=−t+C=−arccosx+C
故可得出结论,
arcsinx+arccosx=C(C为常数)
不妨令x=0,则计算得出C=2π,即
arcsinx+arccosx=2π
总结
还有更多关于形如x2−a2,a2−x2,x2+a2,x2+a2,x2−a2,a2−x2及其它们的倒数形式,它们均可通过三角换元转化成三角函数,反三角函数,通过双曲换元转化成双曲函数,反双曲函数形式下的积分(有关双曲换元的积分方法有兴趣的读者可自行探究),这些公式之间能够相互联系,相互推导,体现了数学的统一之美。有兴趣的读者可以证明更多本文未提到的公式,并能够用更多方式去证明这些公式,使得公式之间相互推导。
同时某些积分公式虽然看起来相当复杂,但是可以通过赋予其几何意义直观得出,虽然不能用于严谨的积分公式的推导,但是可以辅助大家记忆他们。真正体现了我国数学家华罗庚先生所说的“数缺形时少直观,形少数时难入微;数形结合百般好,隔离分家万事休”。